[Python 자료구조 #트리3] 힙(Heap), 허프만 코드

Programming 기초/Python

[Python 자료구조 #트리3] 힙(Heap), 허프만 코드

코딩상륙작전 2023. 5. 25. 21:45

* 힙(Heap)

사전상 의미는 "더미". 컴퓨터 분야에서 힙은 "더미"와 모습이 비슷한 완전이진트리 기반의 자료 구조를 의미한다.
힙은 여러 개의 값들 중에서 가장 큰(또는 작은) 값을 빠르게 찾아내도록 만들어진 자료 구조이다.
큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있도록 하는 정도의 느슨한 정렬 상태만을 유지.
최대 힙(max heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전이진트리

(key(부모노드)≥key(자식노드))

최소 힙(min heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전이진트리

(key(부모노드)≤key(자식노드))

* 힙 트리 삽입 연산

힙에 새로운 항목을 삽입할 때 힙의 순서 특성(최대 힙, 최소 힙)과 트리의 형태적 특성(완전이진트리)을 반드시 유지해야한다.

>> sift-up 또는 up-heap

마지막 노드로 삽입된 새 항목은 루트 노드까지의 경로에 따라 적절한 위치를 찾을 때까지 부모노드와 교환하면서 위로 올라간다.
최악의 경우 트리의 높이에 해당하는 비교 연산 및 이동 연산이 필요하므로 (힙의 높이는 log_2 n이므로) 시간 복잡도는 O(log_2 n)이다.

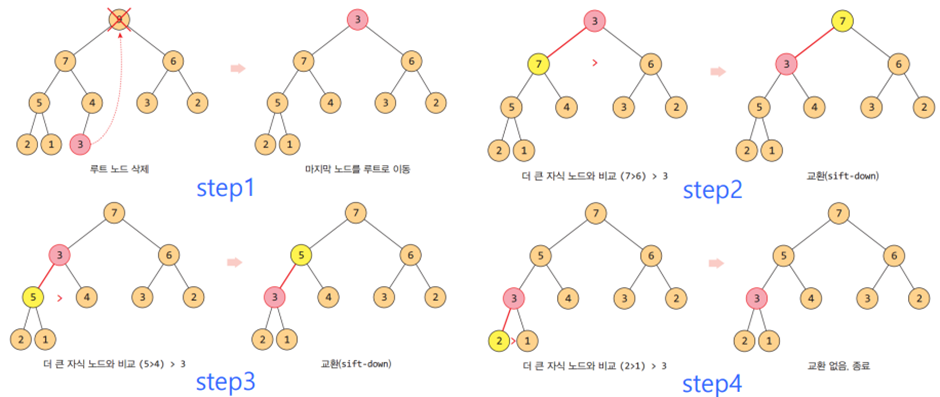
* 힙 트리 삭제 연산

>> sift-down 또는 down-heap

루트 노드에 마지막 노드를 올린다. 이렇게 하면 완전이진트리 조건은 만족하지만 힙의 순서 특성은 만족하지 않는다.
루트 노드를 자식과 비교하여 자식이 더 크면 교환한다. 이때, 자식들 중에서 더 큰 자식이 교환 후보가 된다. 이 과정을 자식이 없거나 자식이 더 작을 때까지 반복한다.
새로운 루트와 자식 노드들을 비교한다. 이때 최대 힙에서는 반드시 더 큰 노드와 비교해야 한다. 최소 힙에서는 더 작은 노드와 비교한다.

최악의 경우 트리의 높이에 해당하는 비교 연산 및 이동 연산이 필요하므로 (힙의 높이는 log_2 n이므로) 시간 복잡도는 O(log_2 n)이다.

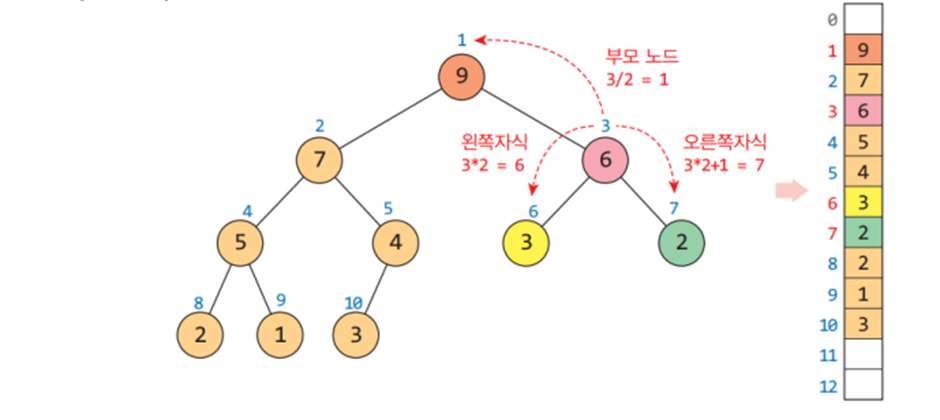
* 배열을 이용한 힙의 표현

힙을 저장하는 효과적인 자료구조는 배열이다.
프로그램 구현이 쉽도록 배열의 첫 번째 인덱스 0은 사용하지 않는다.

배열로 힙을 표현하면 자식과 부모 노드의 위치(인덱스)를 쉽게 계산할 수 있다. 어떤 노드의 부모나 왼쪽, 오른쪽 자식노드의 위치는 다음과 같이 계산된다.
부모의 인덱스 = (자식의 인덱스)/2
왼쪽 자식의 인덱스 = (부모의 인덱스)*2
오른쪽 자식의 인덱스 = (부모의 인덱스)*2 + 1

* 최대 힙의 구현

class MaxHeap:          # 최대 힙 클래스
    def __init__(self):      # 생성자
        self.heap = []       # 리스트(배열)를 이용한 힙
        self.heap.append(0)      # 0번 항목은 사용하지 않음

    def size(self):           # 힙의 크기
        return len(self.heap) - 1  

    def isEmpty(self):          # 공백 검사
        return self.size() == 0  

    def Parent(self, i):        # 부모노드 반환
        return self.heap[i // 2]  

    def Left(self, i):       # 왼쪽 자식 반환
        return self.heap[i * 2]     

    def Right(self, i):         # 오른쪽 자식 반환
        return self.heap[i * 2 + 1]

    def display(self, msg="힙 트리: "):
        print(msg, self.heap[1:])   # 슬라이싱 이용

    def insert(self, n):
        self.heap.append(n)     # 맨 마지막 노드로 일단 삽입
        i = self.size()         # 노드 n의 위치
        while i != 1 and n > self.Parent(i):       # 부모보다 큰 동안 계속 up-heap
            self.heap[i] = self.Parent(i)       # 부모를 끌어내림
            i = i // 2          # i를 부모의 인덱스로 올림
        self.heap[i] = n        # 마지막 위치에 n 삽입

    def delete(self):       # 루트 노드를 삭제하는 연산
        parent = 1      # 부모 노드 인덱스
        child = 2       # 왼쪽자식 노드 인덱스(오른쪽 자식 노드 인덱스는 +1 해주면 된다.)
        if not self.isEmpty():
            hroot = self.heap[1]        # 삭제할 루트를 복사해 둠. 
            last = self.heap[self.size()]   # 마지막 노드
            while child <= self.size():     # 마지막 노드 이전까지
                # 만약 오른쪽 노드가 더 크면 child를 1증가 (기본은 왼쪽 노드)
                if child < self.size() and self.Left(parent) < self.Right(parent):  # MinHeap이었으면 Left > Right
                    child += 1  
                if last >= self.heap[child]:    # 오른쪽 왼쪽 자식 비교를 통해 구해진 더 큰 자식이 마지막 노드 보다 더 작으면
                    break           # 삽입 위치를 찾음. down-heap 종료 아니면 down-heap 계속.
                self.heap[parent] = self.heap[child]    # 부모노드에 자식 노드의 값을 넣음.
                parent = child  # 새 탐색 시 사용할 부모 노드 인덱스를 갱신
                child *= 2      # 왼쪽 자식의 인덱스 = (부모 인덱스) * 2로 갱신

            self.heap[parent] = last    # 맨 마지막 노드를 parent 위치에 복사
            self.heap.pop(-1)       # 맨 마지막 노드 삭제
            return hroot        # 저장해두었던 루트를 반환

heap = MaxHeap()
data = [2, 5, 4, 8, 9, 3, 7, 3]
print("[삽입 연산]: ", data)
for elem in data:
    heap.insert(elem)
heap.display("[ 삽입 후 ]: ")
heap.delete()
heap.display("[ 삭제 후 ]: ")
heap.delete()
heap.display("[ 삭제 후 ]: ")
-------------------------------------
[삽입 연산]:  [2, 5, 4, 8, 9, 3, 7, 3]
[ 삽입 후 ]:  [9, 8, 7, 3, 5, 3, 4, 2]
[ 삭제 후 ]:  [8, 5, 7, 3, 2, 3, 4]   
[ 삭제 후 ]:  [7, 5, 4, 3, 2, 3]

* 다양한 방법으로 구현한 우선순위 큐의 성능 비교

표현방법	삽입	삭제	탐색
정렬 안 된 배열	O(1)	O(n)	O(n)
정렬된 배열	O(n)	O(1)	O(1)
힙	O(log_2 n)	O(log_2 n)	O(1)

우선순위 큐를 구현하는 가장 좋은 방법은 힙이다. 최악의 경우도 O(log_2 n)의 시간을 보장해 주기 때문이다.

파이썬에는 힙을 지원하는 heapq 모듈이 있다. 이 모듈에는 리스트를 힙으로 변경하는 heapify() 함수를 지원한다. 단, 이 함수는 최소힙을 만든다. 사용 예는 다음과 같다.

import heapq
arr = [ 5, 3, 8, 4, 9, 1, 6, 2, 7 ]
print(arr)
heapq.heapify(arr)
print(arr)
print(heapq.heappop(arr))
print(heapq.heappop(arr))
print(heapq.heappop(arr))
print(arr)

------------------------------------------------

[5, 3, 8, 4, 9, 1, 6, 2, 7]
[1, 2, 5, 3, 9, 8, 6, 4, 7]
1
2
3
[4, 6, 5, 7, 9, 8]

* 힙의 응용 : 허프만 코드(Huffman codes)

흔히 사용하는 아스키 코드는 모든 문자를 동일한 비트수로 표현하는데, 압축의 관점에서는 비효율적이다.
자주 사용되는 문자에는 적은 비트수를 부여하고 그렇지 않은 문자에는 많은 비트수를 부여해 문서의 크기를 줄일 수 있기 때문이다.
데이터를 압축할 때는 아스키 코드와 같은 고정길이 코드를 사용하지 않고 가변길이 코드를 흔히 사용한다.

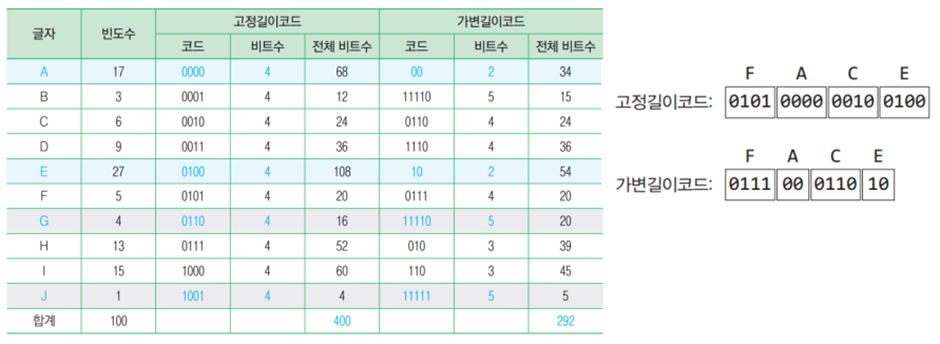
"FACE"란 단어의 경우 위 그림과 같이 표현된다.
고정길이 코드에서는 0101 0000 0010 0100과 같이 순서대로 4비트씩 끊어서 코드를 적거나 읽으면 된다.
가변 길이 코드로 코딩된 0111000111010는 어떻게 해독할까? 한 비트씩 읽으면서 테이블에 코드가 있으면 한 문자로 처리한다.
이런 해독과정을 가능하려면 위의 표와 같이 모든 가변길이코드가 다른 코드의 첫 부분이 아니어야 한다. 따라서 코딩된 비트열을 왼쪽에서 오른쪽으로 조사해 보면 정확히 하나의 코드만 일치하는 것을 알 수 있다. 이런 종류의 코드를 허프만 코드(Huffman codes)라고 하고, 허프만 코드를 만들기 위하여 이진트리를 사용할 수 있다.

* 허프만 코드 생성 방법

단순화를 위해 문자는 's', 'i', 'n', 't', 'e' 만 사용하고, 빈도수가 각각 4, 6, 8, 12, 15로 주어졌다고 하자.

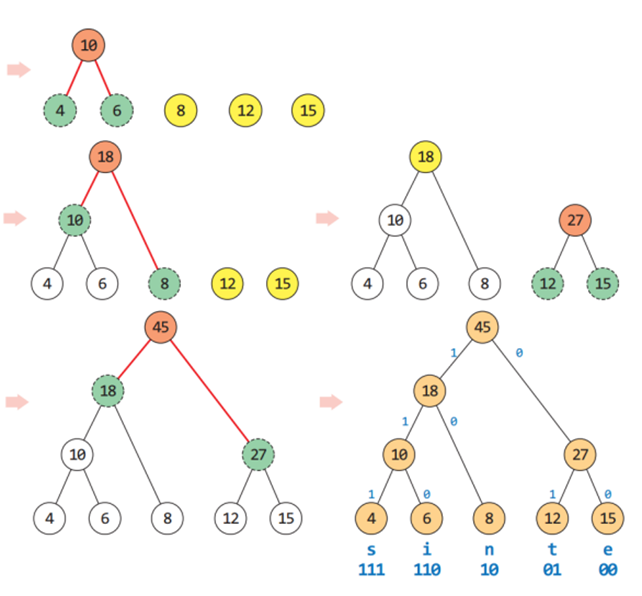
단계 : 각 문자별로 노드를 생성. 노드의 값은 빈도수가 됨. 각 노드는 모두 독립적인 트리의 루트가 됨.
단계 : 가장 작은 빈도수의 두 노드를 찾아 묶어 이진트리를 구성. 이때 루트의 값은 자식 노드의 값의 합이 됨.
단계 : 남은 트리에서 가장 작은 빈도수의 루트를 2개 찾아 묶어 이진트리를 구성.(18,12, 15 남음)
단계 : 남은 트리에 대해서도 동일한 처리를 함. (18, 27 루트의 트리 2개 남음)
단계 : 마지막으로 18과 27을 묶음. 최종 허프만 트리는 1개가 됨.
단계 : 마지막으로 코드를 할당함. 트리에서 왼쪽 간선은 비트 1을 나타내고 오른쪽 간선은 비트 0을 나타낸다고 하고, 루트에서부터 그 노드로 이동하면서 코드를 순서대로 적으면 각 문자별로 최종 코드가 됨.

MinHeap 클래스 코드 참고.

class MinHeap: # 최대 힙 클래스

def __init__(self): # 생성자

self.heap = [] # 리스트(배열)를 이용한 힙

self.heap.append(0) # 0번 항목은 사용하지 않음

def size(self): # 힙의 크기

return len(self.heap) - 1

def isEmpty(self): # 공백 검사

return self.size() == 0

def Parent(self, i): # 부모노드 반환

return self.heap[i // 2]

def Left(self, i): # 왼쪽 자식 반환

return self.heap[i * 2]

def Right(self, i): # 오른쪽 자식 반환

return self.heap[i * 2 + 1]

def display(self, msg="힙 트리: "):

print(msg, self.heap[1:]) # 슬라이싱 이용

def insert(self, n):

self.heap.append(n) # 맨 마지막 노드로 일단 삽입

i = self.size() # 노드 n의 위치

while i != 1 and n < self.Parent(i): # 부모보다 작은 동안 계속 up-heap

self.heap[i] = self.Parent(i) # 부모를 끌어내림

i = i // 2 # i를 부모의 인덱스로 올림

self.heap[i] = n # 마지막 위치에 n 삽입

def delete(self): # 루트 노드를 삭제하는 연산

parent = 1 # 부모 노드 인덱스

child = 2 # 왼쪽자식 노드 인덱스(오른쪽 자식 노드 인덱스는 +1 해주면 된다.)

if not self.isEmpty():

hroot = self.heap[1] # 삭제할 루트를 복사해 둠.

last = self.heap[self.size()] # 마지막 노드

while child <= self.size(): # 마지막 노드 이전까지

# 만약 오른쪽 노드가 더 작으면 child를 1증가 (기본은 왼쪽 노드)

if child < self.size() and self.Left(parent) > self.Right(parent): # MinHeap이었으면 Left > Right

child += 1

if last <= self.heap[child]:

# 오른쪽 왼쪽 자식 비교를 통해 구해진 더 작은 자식이 마지막 노드 보다 더 작으면

break # 삽입 위치를 찾음. down-heap 종료 아니면 down-heap 계속.

self.heap[parent] = self.heap[child] # 부모노드에 자식 노드의 값으로 갱신.

parent = child # 새 탐색 시 사용할 부모 노드 인덱스를 갱신

child *= 2 # 왼쪽 자식의 인덱스 = (부모 인덱스) * 2로 갱신

self.heap[parent] = last # 맨 마지막 노드를 parent 위치에 복사

self.heap.pop(-1) # 맨 마지막 노드 삭제

return hroot # 저장해두었던 루트를 반환

import MinHeap


def make_tree(freq):    # 각 문자의 빈도수를 입력 받아 모든 노드를 힙에 삽입한다.
    heap = MinHeap.MinHeap()  # 최소 힙 생성. import로 불러왔기에 파일명.함수 형식을 지켜야 한다.
    for n in freq:
        heap.insert(n)

    for i in range(1, len(freq)):
        e1 = heap.delete() 
        e2 = heap.delete()
        heap.insert(e1 + e2)
        print(" (%d+%d)" % (e1, e2))


label = ["E", "T", "N", "I", "S"]
freq = [15, 12, 8, 6, 4]    # 전체 문자의 수가 n개인 경우 이 과정을 n-1번 실행하면 최종적으로 허프만 코드가 만들어진다.
make_tree(freq)
----------------------------------------------------------
 (4+6)
 (8+10)
 (12+15)
 (18+27)

최소 빈도수의 노드들이 합해지는 과정까지만 작성되었다.
이 프로그램에서 만들어진 트리에서 각 문자별 가변길이 코드를 만들기 위해서는 추가적인 코드가 필요할 것이다.