Programming 기초/Python
[Python 자료구조 #그래프2] 그래프의 탐색(DFS, BFS), 연결 성분 검사
코딩상륙작전
2023. 5. 27. 14:15
* 그래프의 탐색 - 깊이 우선 탐색
- 깊이 우선 탐색(Depth First Search, DFS)은 스택을 이용한 미로 탐색과 유사하다.(이전 포스팅 참고)
- 탐색 과정에 이미 방문한 정점을 관리하는 집(또는 리스트)가 필요한데, 이를 visited라 하면 맨 처음에는 visited가 공집합이어야 한다.
- 가장 최근에 만났던 갈림길로 되돌아가야 하므로 스택을 사용하여 구현할 수 있지만, 순환의 형태로 구현하는 것이 더 직관적이다.
- 그래프가 인접리스트로 표현되어 있으면 O(n + e) 이고(n은 노드 수 e는 간선 수), 인접 행렬로 표시되어 있다면 O(n^2)이다.

# 인접 리스트 방식으로 표현된 그래프를 활용한 dfs. 인접행렬을 이용하면 달라짐
# 매개 변수로 그래프, 시작 정점, 그리고 visited를 사용
# dfs가 처음 (인수 없이)호출되면 공백상태의 방문정점 집합 visited를 생성
def dfs(graph, start, visited = set() ):
if start not in visited : # start가 방문하지 않은 정점이면
visited.add(start) # start를 방문한 노드 집합에 추가
print(start, end=' ') # start를 방문했다고 출력함
nbr = graph[start] - visited # nbr(아직 방문하지 않은 인접정점): 차집합 연산 사용
for v in nbr: # v ∈ {인접정점} - {방문정점}
dfs(graph, v, visited) # v에 대해 dfs를 순환적으로 호출* 그래프의 탐색 - 너비 우선 탐색
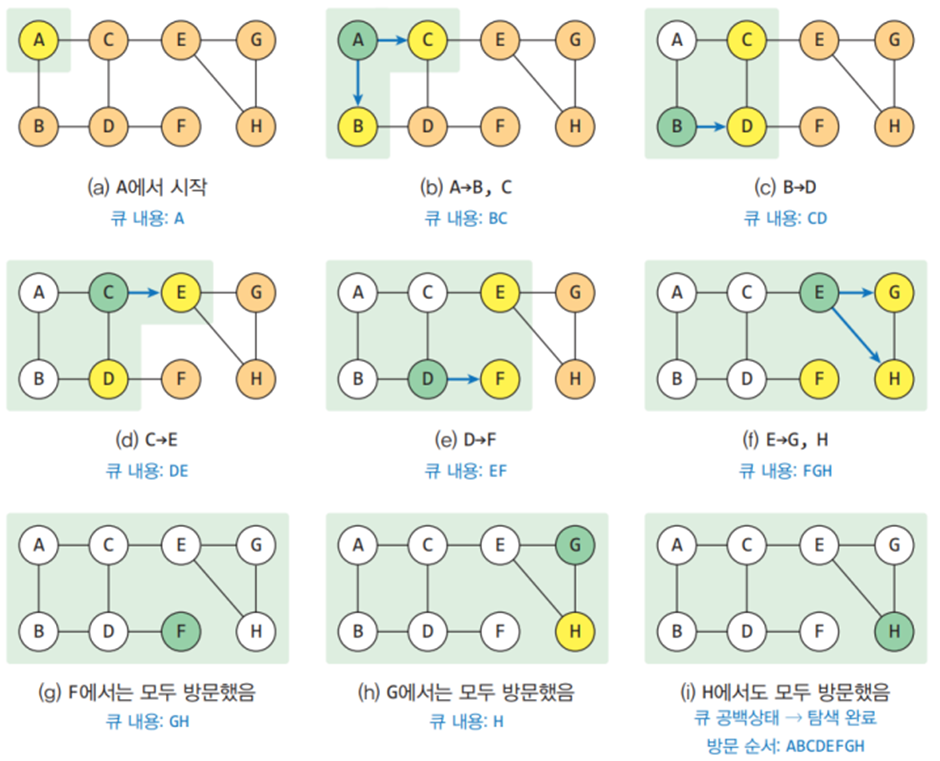
- 너비 우선 탐색(breadth first search : BFS)은 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다.
- 정점들이 방문될 때마다 큐에 인접 정점을 삽입하고, 더 이상 방문할 인접 정점이 없는 경우 큐의 맨 앞에서 정점을 꺼내 그 정점과 인접한 정점들을 차례대로 방문한다.
- 이전 포스팅에서 다룬 CircularQueue를 사용할 수도 있고, 파이썬의 queue 모듈을 사용할 수도 있고, 파이썬의 collections 모듈을 사용할 수도 있다. (여기선 collections 모듈을 사용한다.)
- 너비 우선 탐색은 그래프가 인접 리스트로 표현되어 있으면 전체 수행시간이 O(n + e)이며, 인접행렬로 표현되어 있는 경우는 O(n^2) 시간이 걸린다.
< collections 모듈 >
내장 자료형인 튜플이나 딕셔너리에 대한 확장 데이터 구조들을 제공하는 모듈.
defaultdict, counter, deque, nametuple 등을 제공하는데 deque는 덱에 해당하는 클래스이다.
이름이 길다면 별명을 붙여 사용할 수 있다. import시에 아래와 같이 별명을 붙일 수 있다.
import collections as cols
너비우선탐색에서는 덱을 큐처럼 사용한다.(collections에서는 덱의 전단과 후단을 left / right로 명명한다.)
deque( [ ] ) : 덱 객체를 생성하고 리스트 항목을 이용해 초기화
append() / pop () : 덱의 우측 끝(후단)에 항목 추가/ 삭제
appendleft() / popleft() : 덱의 좌측 끝(전단)에 항목 추가/삭제
import collections # collections 모듈 불러오기
def bfs(graph, start):
visited = set([start]) # 맨 처음에는 start만 방문한 정점임
queue = collections.deque([start]) # 컬렉션의 덱 객체 생성(큐로 사용)
while queue: # 공백이 아닐 때 까지
vertex = queue.popleft() # 큐에서 하나의 정점 vertex를 빼냄
print(vertex, end=' ') # vertex는 방문했음을 출력
nbr = graph[vertex] - visited # nbr : 차집합 연산 이용
for v in nbr: # v ∈ {인접정점} - {방문정점}
visited.add(v) # 이제 v는 방문했음
queue.append(v) # v를 큐에 삽입
* 연결 성분 검사
- 연결 성분(connected component)이란 최대로 연결된 부분 그래프를 말한다.
- 그림의 그래프에는 2개의 연결된 부분 그래프, 즉 2개의 연결 성분이 있다.

▶ BFS나 DFS를 이용하여 연결 성분을 찾을 수 있다. (여기서는 DFS를 사용한다.)
- 그래프의 임의의 정점을 선택.
- 깊이우선탐색(DFS)를 통해 연결되어 있는 모든 정점들 출력.
- 더 이상 연결된 정점이 없으면 그래프에서 아직 방문되지 않은 다른 정점을 선택해 동일 과정 되풀이.
- 이 과정을 그래프의 모든 정점이 방문될 때까지 반복.
# 연결 성분 검사 함수
def find_connected_component(graph) :
visited = set() # 이미 방문한 정점 집합
colorList = [] # 부분 그래프별 정점 리스트
# vtx : 방문하지 않은 정점
# 그래프 탐색 dfs_cc()를 이용하여
# vtx와 연결된 모든 정점의 리스트 color를 만들고
# 이를 부분 그래프 리스트 colorlist에 추가한다.
for vtx in graph : # 그래프의 모든 정점들에 대해
if vtx not in visited : # 방문하지 않은 정점이 있으면
color = dfs_cc(graph, [], vtx, visited) # 새로운 컬러 리스트 생성
colorList.append( color ) # 컬러 리스트 추가
print("그래프 연결성분 개수 = %d " % len(colorList))
print(colorList) # 정점 리스트들을 출력
# 리스트(colorlist) 안에 리스트(color) 구조의 결과물 출력됨.
#
▶ 그래프 탐색 함수 dfs_cc() 구현
앞에서 구현한 dfs()를 약간 수정하여 구현. 변경된 부분은 다음과 같다.
- dfs 함수에 매개변수 하나를 추가한다. 현재 연결된 정점 리스트 color이다.
- visited는 처음 호출될 때 제공되므로 디폴트 인자를 사용하지 않았다.
- 정점 리스트 color에 현재 정점을 삽입한다.
- 처리가 끝나면 정점 리스트 color를 반환해야 한다.
↓dfs 비교
더보기
def dfs(graph, start, visited = set() ):
if start not in visited : # start가 방문하지 않은 정점이면
visited.add(start) # start를 방문한 노드 집합에 추가
print(start, end=' ') # start를 방문했다고 출력함
nbr = graph[start] - visited # nbr(아직 방문하지 않은 인접정점): 차집합 연산 사용
for v in nbr: # v ∈ {인접정점} - {방문정점}
dfs(graph, v, visited) # v에 대해 dfs를 순환적으로 호출
# 그래프 탐색 함수 dfs_cc() 구현 -> 해당 vertex가 속한 연결 성분의 리스트를 반환
def dfs_cc(graph, color, vertex, visited):
if vertex not in visited : # 아직 칠해지지 않은 정점에 대해
visited.add(vertex) # 이제 방문했음
color.append(vertex) # 같은 색의 정점 리스트에 추가
nbr = graph[vertex] - visited # nbr: 차집합 연산 이용
for v in nbr: # v ∈ {인접정점} - {방문정점}
dfs_cc(graph, color, v, visited) # 순환 호출
return color # 같은 색의 정점 리스트 반환
# 위 그림의 그래프를 앞서 만든 함수를 이용해 연결성분을 찾는 코드와 결과이다.
mygraph1 = {
"A": set(["B", "C"]),
"B": set(["A"]),
"C": set(["A"]),
"D": set(["E"]),
"E": set(["D"]),
}
print("find_connected_component: ")
find_connected_component(mygraph1)
---------------------------------------
find_connected_component:
그래프 연결성분 개수 = 2
[['A', 'C', 'B'], ['D', 'E']]