EMA(Exponential Moving Average, EMA) 지수이동평균

* EMA(Exponential Moving Average, EMA) 지수 이동 평균

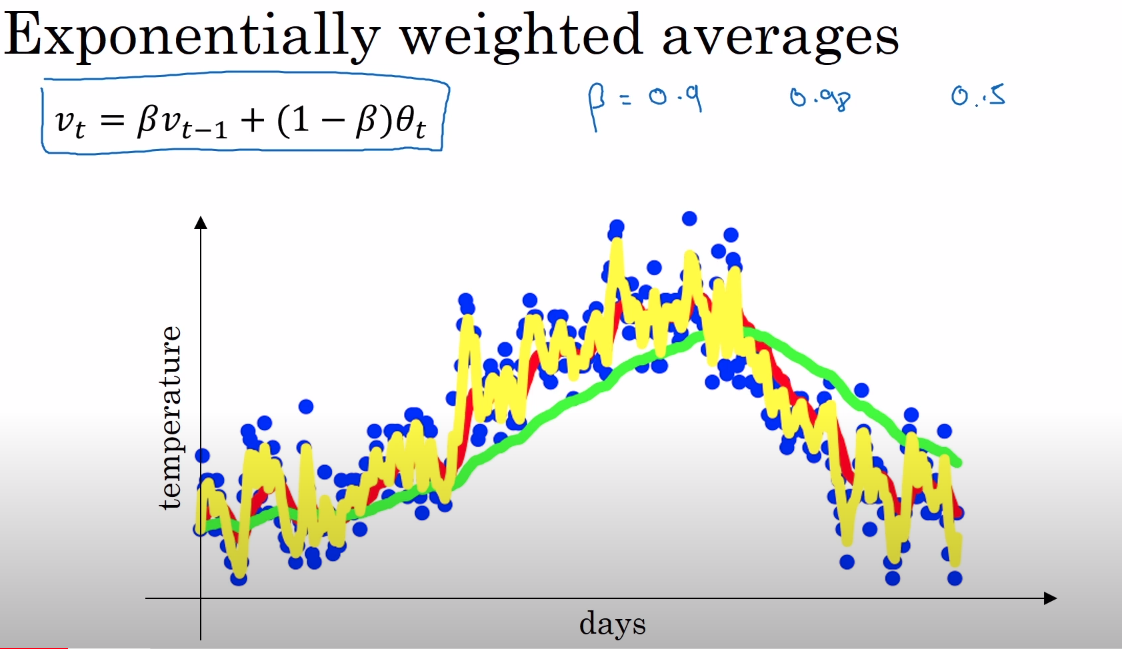
https://www.youtube.com/watch?v=NxTFlzBjS-4&list=PLkDaE6sCZn6Hn0vK8co82zjQtt3T2Nkqc&index=18

각 날짜별 온도를 가지고 지수이동평균을 구하고자 한다.

현재의 지수이동평균값은 과거의 온도값의 영향에 가중치를 곱해서 구한 값이다. 즉 과거의 영향을 고려해서 값을 표현하고자 할 때 사용되는 것이다.

지수평활법(EMA)이 모든 과거 데이터를 고려하는 반면, 이동평균(MA)은 k개의 과거 데이터 포인트만을 고려한다는 점에서 차이가 있다.

(주식에서 5일 선, 120일 선 등은 MA를 말하는 것이고, 지수평활법에서는 모든 과거 데이터를 고려하므로, 5일 선, 120일 선 등의 표현은 조금 부적절해보인다.)

Andrew Ng의 Deep Learing 강의

 

 

theta는 1~100일의 현재 온도이고,  v는 지수이동평균값을 의미한다. 가중치(혹은 모멘텀) beta를 0.9로 잡아서 "10일" 지수이동평균을 구하는 과정이다.

결론부터 말하자면,
"x 축 : 시간, y축 : theta의 계수"인 그래프를 그렸을 때, theta의 계수 값이 1/e배로 감소하는데 걸리는 일 수(day)를 "00일" 지수이동평균 이라고 부른다.
 예를 들어 beta를 0.98로 설정하면, 시간과 theta의 계수에 대한 그래프를 그렸을 때, theta의 계수 값이 1/e배로 감소하는데 걸리는 시간은  50일(t=1/(1-beta)=1/(1-0.98)=50)이고, 이를 50일 지수이동평균이라고 부른다. 

 

$V_t = \beta V_{t-1} + (1-\beta)\theta_t$ 의 $v_t$는 이전 $\theta$값의 영향을 $\beta$만큼 반영한 가중치 평균값이다.

예를들어 $\beta$ 가 0.9라고 할 때, $\frac 1 {1-\beta} =\frac 1 {1-0.9} = 10$ 이고, 

 

 $v_{100} = 0.9 v_{99}+ 0.1 \theta_{100}$

 $v_{99} = 0.9 v_{98}+ 0.1 \theta_{99}$

 $v_{98} = 0.9 v_{97}+ 0.1 \theta_{98}$

 $v_{97} = 0.9 v_{96}+ 0.1 \theta_{97}$

 $v_{96} = 0.9 v_{95} + 0.1 \theta_{96}$

...

$v_0 = 0$

에서 $v_100$에 $v_1$ ~ $v99$ 를 대입해보자.

$v_{100} = 0.9(0.9V_{98} + 0.1 \theta_{99}$) + 0.1 \theta_{100}$

...

정리해주면 아래와 같다.

$v_{100} = 0.1\cdot\theta_{100} + 0.1\cdot0.9^1\theta_{99} + 0.1\cdot(0.9)^2\theta_{98} + 0.1\cdot(0.9)^3\theta_{97} + ... + 0.1\cdot(0.9)^{99}\theta_1$

위 식은 $\theta$에 대한 값과  $0.1\cdot(\beta)^{100-t}$ 값을 element-wise product(요소별곱셈)한 것인데, 

$\theta$의 계수인 $0.1\cdot(\beta)^{100-t}$ 부분만 살펴보면, t가 커질수록 지수적으로 증가하는 지수그래프 꼴이다.

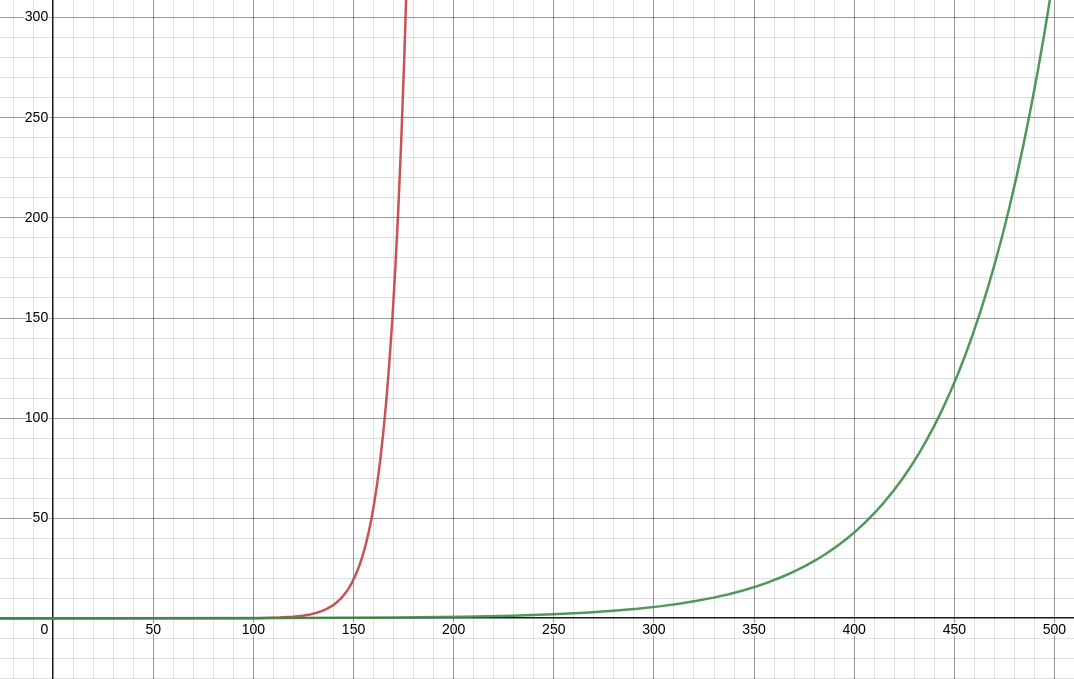
x=100이전까지는 초록선의 y값이 더 크다.

0.1까지의 그래프가 잘 안 보이므로 그래프를 확대 및 과장해서 그리면 아래와 같다.

조금 더 직관적으로 이해하기 위해 $\beta$의 값에 따른 의 변화를 $\theta$의 계수의 변화를 살펴보고 최종적으로 지수평균값 v의 변화를 살펴보자.
$(1-\epsilon)^{\frac 1 {\epsilon}} \simeq \frac 1 e$임을 이용해서  지수평균값v를 어림잡아 계산할 수 있다.

 

예를 들어 beta를 0.9로 설정하면, $\theta$의 계수 값이 $\frac1 e$로 감소하는데 걸리는 시간은  10일($t \simeq \frac1 {1-\beta}=\frac1 {1-0.9} =10$)이다. 

 

또한 beta를 0.98로 설정하면, 시간과 theta의 계수에 대한 그래프를 그렸을 때, $\theta$의 계수 값이 $\frac1 e$배로 감소하는데 걸리는 시간은  50일($t \simeq \frac1 {1-\beta}=\frac1 {1-0.98}=50$)이다.

 

( 왜 $\frac1 e$배 감소하는 지점을 기준으로 잡는가? - 모르겠다... )

$\frac1 e$배로 감소하는 지점을 기준으로 잡는 이유는 잘 모르겠다. 위키피디아에서 그 부분을 기준으로 잡는다고만 설명하는 것 같다.

https://en.wikipedia.org/wiki/Exponential_smoothing

 

 

초록 선이 $y=0.1\cdot0.98^{100-t}$이다. 

빨간 선이 $y=0.1\cdot0.9^{100-t}$이고,

 

 

 

지수평균값은 $\theta$와 $\theta$의 계수 값의 요소곱임을 상기해서 위 결과를 아래 식과 연결시켜 생각해보자.

 

$v_{100} = 0.1\cdot\theta_{100} + 0.1\cdot0.98^1\theta_{99} + 0.1\cdot(0.98)^2\theta_{98} + 0.1\cdot(0.98)^3\theta_{97} + ... + 0.1\cdot(0.98)^{99}\theta_1$

 

$v_{100} = 0.1\cdot\theta_{100} + 0.1\cdot0.9^1\theta_{99} + 0.1\cdot(0.9)^2\theta_{98} + 0.1\cdot(0.9)^3\theta_{97} + ... + 0.1\cdot(0.9)^{99}\theta_1$

 

$\beta=0.98$일 때는 $\theta_{50}$에서의 계수가 $0.1\cdot\frac1 e$이고,

$\beta=0.9$일 때는 $\theta_{90}$에서의 계수가 $0.1\cdot\frac1 e$이다.

 

$\beta$가 커질수록 $\theta$의 계수가 감소하는데 오래 걸린다는 말이고, 최근 정보($\theta$가 큰 순)에 더 큰 가중치를 부여한다는 뜻이다. 즉 먼 과거의 정보는 서서히 잊고 새로운 정보를 크게 반영한다. (다시 말하면, 과거 정보의 반영 규모를 기하급수적으로 감소시킨다.)

 

 

2023.09.12 - [Machine Learning] - [DL] Gradient Descent Methods

[DL] Gradient Descent Methods

Adam의 수식을 가져와서 지수이동평균의 관점에서 분석해보자.

Adam

$$W_{t+1} = W_t - \frac {\eta} {\sqrt{v_t+\epsilon}} \frac {\sqrt{1-\beta_2^2}} {1-\beta_1^t} m_t$$

$v_t = \beta_2v_{t-1} + (1-\beta_2)g_t^2$ 에서 $g_t^2$는 gradient 값을 제곱한 값인데,

$\frac {1} {\sqrt{v_t+\epsilon}}$에서 분모에 EMA of gradient squares값은 Adagrad의 $G_t$와 닮았다.

Adagrad

$\frac 1 {\sqrt{G_t+\epsilon}}$와 $\frac 1 {\sqrt{v_t+\epsilon}}$는 많이 변화시켰던 파라미터는 적게 변화시키고, 적게 변화시켰던 파라미터는 많이 변화시키는 방법인데, Adagrad의 문제는 $G_t$(sum of gradient squres)가 많이 학습된 이후에는 그 값이 매우 커지기 때문에 분모가 무한대로 가면서 학습이 안 되는 것이다. 하지만 Adam의 $v_t$은 과거의 정보는 서서히 잊고 새로운 정보를 크게 반영하는 지수이동평균을 썼기 때문에 분모가 무한히 커지지 않는다. 

또한 모멘텀 개념에도 지수이동평균을 적용해서, 최근의 정보를 더 크게 반영하면서 모멘텀의 학습 관성효과를 얻는다.