-
[Python 자료구조 #트리1] 이진 트리, 전위/중위/후위/레벨 순회Programming 기초/Python 2023. 5. 25. 00:21
* 트리(Tree)
- 계층적인 관계를 가진 자료의 표현에 유용한 자료구조가 트리(tree)이다.
- 리스트나 스택, 큐, 덱 등은 모두 자료들이 일렬로 나열된 형태인 선형 자료 구조이다. 트리는 계층적인 구조(hierarchical structure)이다.
- 트리는 순환적으로 정의된다.
- 활용 : 폴더 구조, 효율적인 탐색을 위한 탐색트리, 우선순위 큐를 위한 힙 트리, 인공지능 문제에서 의사결정 구조를 표현하기 위한 결정 트리(decision tree) 등
* 트리의 용어
- 루트(root) 노드: 계층적인 구조에서 가장 높은 곳에 있는 노드, 트리에서 모든 노드는 자신의 서브트리의 루트 노드이다.
- 간선 또는 에지(edge): 노드와 노드를 연결하는 선
- 부모(parent) 노드와 자식(child) 노드 : 간선으로 직접 연결된 노드 중에 상위노드와 하위 노드
- 형제(sibling) 노드: 동일한 부모노드를 가진 노드
- 조상(ancestor) 노드와 자손(descendent) 노드: 어떤 노드에서 루트 노드까지의 경로상에 있는 모든 노드들과 어떤 노드 하위에 연결된 모든 노드
- 단말(terminal, leaf) 노드: 자식 노드가 없는 노드, 자식이 있으면 비단말 노드
- 노드의 차수(degree): 어떤 노드가 가지고 있는 자식의 수
- 트리의 차수: 트리가 가지고 있는 노드의 차수 중에서 가장 큰 차수
- 레벨(level): 트리의 각층에 번호를 매기는 것. 루트의 레벨은 1이 되고 한 층씩 내려갈수록 1씩 증가
- 트리의 높이(height): 트리가 가지고 있는 최대 레벨
- 포리스트(forest): 트리들의 집합

출처 : 파이썬으로 쉽게 풀어쓴 자료구조 * 일반 트리
- 노드들이 임의의 개수의 자식을 가질 수 있는 트리
- 노드는 항목 값을 저장하는 데이터 필드와 자식 노드를 가리키는 여러 개의 링크를 갖는다.
* 이진 트리(binary tree)
- 모든 노드가 2개의 서브 트리를 갖는 트리이다. 이때 서브 트리는 공집합일 수도 있다.
- 자식들 사이에도 순서가 존재한다.
class TNode: # 이진트리를 위한 노드 클래스 def __init__ (self, data, left, right): # 생성자 self.data = data # 노드의 데이터 self.left = left # 왼쪽 자식을 위한 링크 self.right = right # 오른쪽 자식을 위한 링크* 이진 트리의 종류
- 포화이진트리(full binary tree) : 트리의 각 레벨에 노드가 꽉 차있는 이진트리
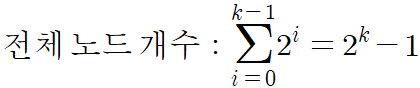
- 완전이진트리(complete binary tree) : 높이가 k인 트리에서 레벨 1부터 k-1까지는 노드가 모두 채워져 있고 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리. 마지막 레벨에서는 노드가 꽉차있지 않아도 되지만 중간에 빈곳이 있으면 안 된다. 포화이진트리는 완전이진트리이다.
* 이진트리의 성질
- 간선의 개수 : n개의 노드를 가진 트리는 n-1개의 간선을 가진다.
- 높이가 h인 이진트리는 h개 이상, 2^h-1개 이하의 노드를 가진다.
- n개의 노드를 가지는 이진트리의 높이(h)는 [log_2 (n+1)]이상이고 n이하이다.
* 트리의 모든 노드를 방문하는 방법
- 트리를 순회(traversal)한다는 것은 트리에 속하는 모든 노드를 한 번씩 방문하여 노드의 데이터를 목적에 맞게 처리하는 것을 의미한다.
1. 전위 순회(preorder traversal) : VLR, 루트를 먼저 방문하고 그 다음에 왼쪽 서브트리 방문하고 오른쪽 서브트리를 마지막으로 방문한다.
def preorder(n) : # 전위 순회 함수 if n is not None : print(n.data, end=' ') # 먼저 루트노드 처리(화면 출력) preorder(n.left) # 왼쪽 서브트리 처리 preorder(n.right) # 오른쪽 서브트리 처리2. 중위 순회(inorder traversal) : LVR, 왼쪽 서브트리, 루트, 오른쪽 서브트리 순으로 방문한다.

def inorder(n) : # 중위 순회 함수 if n is not None : inorder(n.left) # 왼쪽 서브트리 처리 print(n.data, end=' ') # 루트노드 처리(화면 출력) inorder(n.right) # 오른쪽 서브트리 처리3. 후위 순회(postorder traversal): LRV, 왼쪽 서브트리, 오른쪽 서브트리, 루트 순으로 방문한다.
def postorder(n) : if n is not None : postorder(n.left) postorder(n.right) print(n.data, end=' ')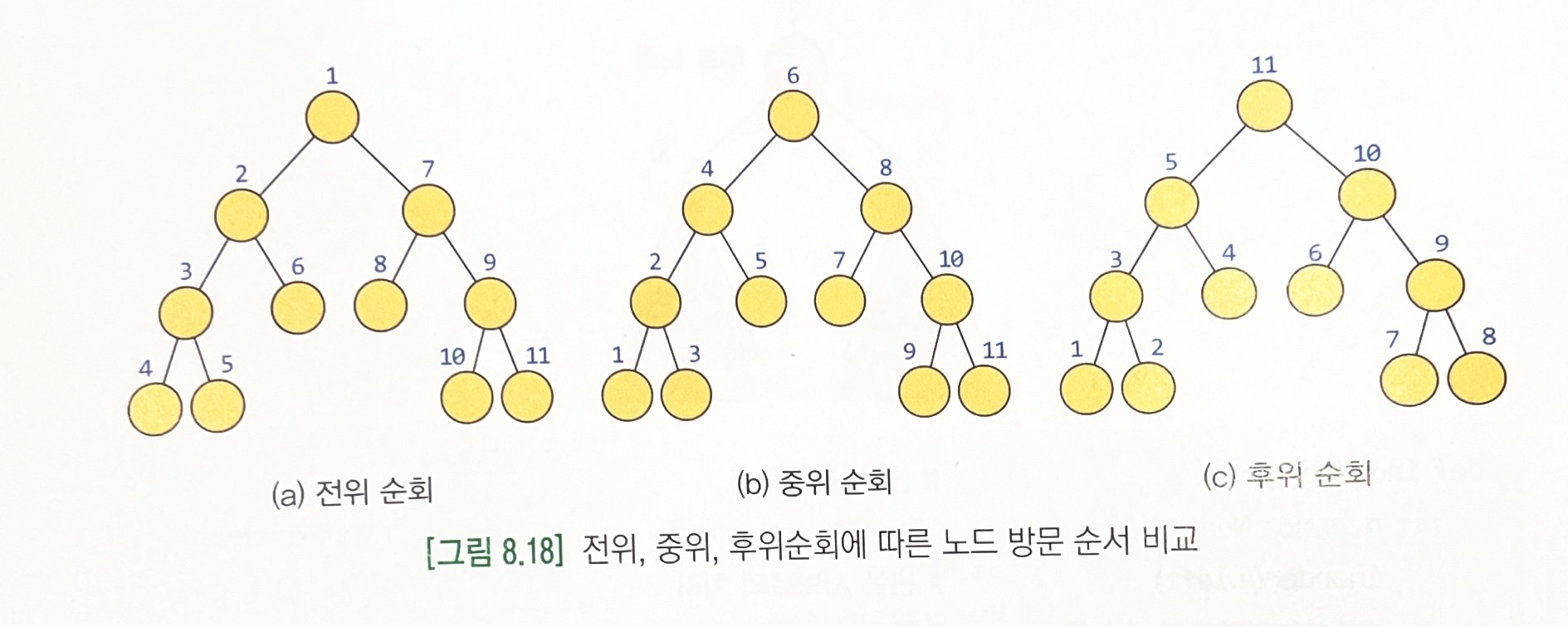
4. 레벨 순회(level order) : 각 노드를 레벨 순으로 검사하는 방법이다. 루트 노드의 레벨이 1이고 아래로 내려갈수록 레벨이 증가한다. 동일한 레벨에서는 좌에서 우로 방문한다. 이러한 레벨 순회에는 큐가 사용된다.
순환은 사용되지 않는다.
def levelorder(root) : queue = CircularQueue() # 큐 객체 초기화 queue.enqueue(root) # 최초에 큐에는 루트 노드만 들어있음. while not queue.isEmpty() : # 큐가 공백상태가 아닌 동안, n = queue.dequeue() # 큐에서 맨 앞의 노드 n을 꺼냄 if n is not None : print(n.data, end=' ') # 먼저 노드의 정보를 출력 queue.enqueue(n.left) # n의 왼쪽 자식 노드를 큐에 삽입 queue.enqueue(n.right) # n의 오른쪽 자식 노드를 큐에 삽입* 노드 개수 구하기
전체 노드의 개수를 세기 위해서는 모든 노드들을 한 번씩 방문해야 한다.
어떤 노드를 루트로 하는 이진트리의 노드의 개수는 왼쪽 서브트리의 노드수와 오른쪽 서브트리의 노드수에 루트 노드의 수(1)을 더하면 된다. 이것은 후위순회 방식의 순환호출이다.
def count_node(n) : # 순환을 이용해 트리의 노드 수를 계산하는 함수. if n is None : # n이 None이면 공백 트리 -> 0을 반환 return 0 else : # 좌우 서브트리의 노드수의 합 +1을 반환(순환이용) return 1 + count_node(n.left) + count_node(n.right)* 단말 노드 개수 구하기
- 단말 노드는 왼쪽자식과 오른쪽 자식이 모두 None인 노드이다.
- 만약 노드 n이 단말 노드이면 1을 반환하면 된다. 단말 노드가 아니면 자신의 두 서브트리의 단말 노드 개수를 순환 호출을 통해 각각 계산하고, 계산된 두 값의 합이 전체 단말 노드의 개수이므로 이를 반환하면 된다.
def count_leaf(n) : if n is None : # 공백 트리 -> 0을 반환 return 0 elif n.left is None and n.right is None : # 단말노드 -> 1을 반환 return 1 else : # 비단말 노드 : 좌우 서브트리의 결과 합을 반환 return count_leaf(n.left) + count_leaf(n.right)* 트리의 높이 구하기
- 트리의 높이도 후위 순회 구조를 사용한다.
- 루트 노드를 포함한 현재 트리의 높이는 좌우 서브트리의 높이 중에서 더 높은 값에 1(루트 노드)을 더한 값이다.
def calc_height(n) : if n is None : # 공백 트리 -> 0을 반환 return 0 hLeft = calc_height(n.left) # 왼쪽 트리의 높이 -> hLeft hRight = calc_height(n.right) # 오른쪽 트리의 높이 -> hRight if (hLeft > hRight) : # 더 높은 높이에 1을 더해 반환. return hLeft + 1 else: return hRight + 1* 테스트 프로그램

d = TNode("D", None, None) e = TNode("E", None, None) b = TNode("B", d, e) f = TNode("F", None, None) c = TNode("C", f, None) root = TNode("A", b, c) print("\n In-Order : ", end="") inorder(root) print("\n Pre-Order : ", end="") preorder(root) print("\n Post-Order : ", end="") postorder(root) print("\nLevel-Order : ", end="") levelorder(root) print() print(" 노드의 개수 = %d개" % count_node(root)) print(" 단말의 개수 = %d개" % count_leaf(root)) print(" 트리의 높이 = %d" % calc_height(root)) --------------------------------------------------- In-Order : D B E A F C Pre-Order : A B D E C F Post-Order : D E B F C A Level-Order : A B C D E F 노드의 개수 = 6개 단말의 개수 = 3개 트리의 높이 = 3'Programming 기초 > Python' 카테고리의 다른 글
[Python 자료구조 #트리3] 힙(Heap), 허프만 코드 (0) 2023.05.25 [Python 자료구조 #트리2] 모르스 코드 결정트리 (0) 2023.05.25 [Python 자료구조 #정렬과 탐색2] 순차탐색, 이진탐색, 보간탐색, 해싱 (0) 2023.05.24 [Python 자료구조 #정렬과 탐색1] 선택정렬, 삽입정렬, 버블정렬, 정렬 응용한 집합 (0) 2023.05.23 [Python 자료구조 #연결리스트3] 이중연결리스트 : 연결된 덱 (0) 2023.05.23