[Python 자료구조 #탐색트리1] 이진탐색트리(BST)

* 이진탐색트리(BST, Binary Search Tree)

• 효율적인 탐색을 위한 이진트리 기반의 자료구조이다.(이진탐색트리는 이진트리의 한 종류이다.)
• 트리의 연산들을 보다 단순하게 설계하기 위해 이진탐색트리에서는 보통 중복을 허용하지 않는다.
• 그렇지만, 필요하다면 중복된 키를 허용할 수도 있다.
• 이진탐색트리의 모든 노드들을 중위 순회로 방문하면 오름차순으로 노드를 방문하게 된다.
• 따라서 어느 정도 정렬된 상태를 유지하고 있다고 볼 수 있다.
• 이진탐색트리는 탐색을 위한 자료구조이므로 노드의 데이터는 하나의 엔트리, (탐색키, 키에 대한 값)의 형태가 되어야 한다.

< 이진탐색트리 정의 >

● 모든 노드는 유일한 키를 갖는다.
● 왼쪽 서브트리의 키들은 루트의 키보다 작다.
● 오른쪽 서브트리의 키들은 루트의 키보다 크다.
● 왼쪽과 오른쪽 서브트리도 이진탐색트리이다.

* 이진 탐색트리를 위한 노드 클래스

class BSTNode:				        # 이진탐색트리를 위한 노드 클래스
    def __init__ (self, key, value):		# 생성자 : 키와 값을 받음
        self.key = key		        	# 키(key)
        self.value = value	          	# 값(value)
        self.left = None		    	# 왼쪽 자식에 대한 링크
        self.right = None			# 오른쪽 자식에 대한 링크

 

* 탐색 연산

1. 키를 이용한 탐색

 

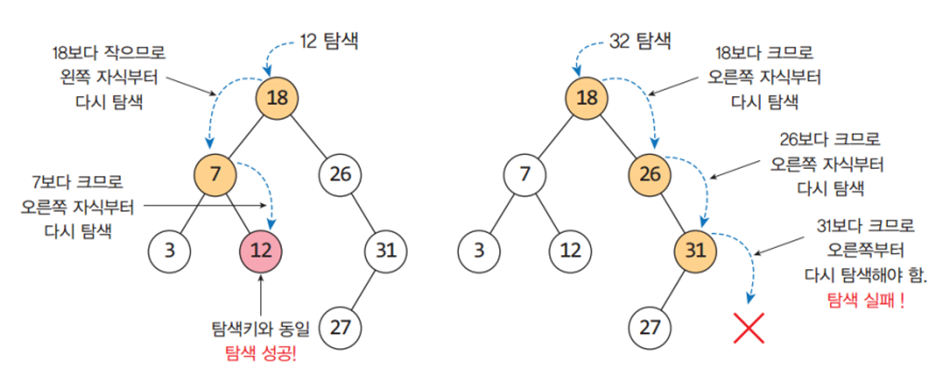
# 순환함수로 구현한 이진탐색트리 탐색연산
def search_bst(n, key) :			# n은 탐색을 시작할 노드, key는 탐색 대상 노드의 key
    if n == None :
        return None
    elif key == n.key:		        	# n의 키 값과 동일 -> 탐색성공
        return n
    elif key < n.key:			        # key<n의 키
        return search_bst(n.left, key)		# 순환호출로 왼쪽 서브트리 탐색
    else:					# key>n의 키
        return search_bst(n.right, key)		# 순환호출로 오른쪽 서브트리 탐색

# 반복 함수로 구현한 이진탐색트리 탐색연산
def search_bst_iter(n, key) :	
    while n != None :				# n이 None이 아닐 때 까지        
        if key == n.key:		        # n의 키 값과 동일 -> 탐색 성공
            return n
        elif key < n.key:		        # key < n의 키
            n = n.left			        # n을 왼쪽 서브트리의 루트로 이동
        else:				        # key > n의 키
            n = n.right			        # n을 오른쪽 서브트리의 루트로 이동
    return None					# 찾는 키의 노드가 없음

 

2. 값을 이용한 탐색

• 트리의 모든 노드를 하나씩 검사한다.
• 순회의 방법에는 제한이 없다.
• 모든 노드를 검사해야하기 때문에 효율이 떨어진다.
• 최악의 경우 시간 복잡도는 O(n)이다.

# 값을 이용한 이진탐색트리 탐색연산(preorder 사용)
def search_value_bst(n, value) :
    if n == None : return None			
    elif value == n.value:			# n의 value와 동일 -> 탐색성공
        return n
    res = search_value_bst(n.left, value) 	# 왼쪽서브트리에서 탐색
    if res is not None :			# 탐색이 성공이면
       return res				# 결과 반환
    else :					# 왼쪽에서 탐색 실패이면
       return search_value_bst(n.right, value)	# 오른쪽을 탐색해 결과 반환

 

3. 최대/최소 키를 가진 노드 탐색

최대 키는 트리의 가장 오른쪽에 있고, 최소 키는 트리의 가장 왼쪽 노드에 있다.

# 반복 구조를 이용한 최대/최소 값 노드 탐색 구현


def search_max_bst(n) :			# 최대 값의 노드 탐색
    while n != None and n.right != None:
        n = n.right
    return n

def search_min_bst(n) :			# 최소 값의 노드 탐색
    while n != None and n.left != None:
        n = n.left
    return n

# 순환구조를 이용한 최대/최소 값 노드 탐색 구현

def search_max_bst(n):
    if n != None and n.right != None:
        n = search_max_bst(n.right)
    return n


def search_min_bst(n):
    if n != None and n.left != None:
        n = search_min_bst(n.left)
    return n

# 위 그림의 이진탐색트리를 간단하게 구현하고 최대/ 최소 값의 노드 탐색 방법 적용

d = BSTNode(3, "D")
d.left = None
d.right = None

e = BSTNode(12, "E")
e.left = None
e.right = None

b = BSTNode(7, "B")
b.left = d
b.right = e

f = BSTNode(27, "F")
f.left = None
f.right = None

c = BSTNode(31, "C")
c.left = f
c.right = None

root = BSTNode(18, "A")
root.left = b
root.right = c

Max_k = search_max_bst(root)
print(Max_k.key, Max_k.value)

Min_k = search_min_bst(root)
print(Min_k.key, Min_k.value)
------------------------------
31 C
3 D

 

* 삽입 연산

삽입할 노드의 키를 이용한 탐색 과정을 수행했을 때 탐색에 실패한 위치가 바로 새로운 노드를 삽입해야 하는 위치이다.

여기서는 키의 중복을 허용하지 않는다.

# 이진탐색트리 삽입연산(노드를 삽입함) : 순환구조 이용 
def insert_bst(r, n):		# r은 루트노드, n은 삽입할 노드
    if n.key < r.key:		# 삽입할 노드의 키가 루트보다 작으면
        if r.left is None:  # 루트의 왼쪽 자식이 없으면
            r.left = n      # n은 루트의 왼쪽 자식이 됨.
            return True
        else:        	   # 루트의 왼쪽 자식이 있으면
            return insert_bst(r.left, n)    # 왼쪽 자식에게 삽입하도록 함(순환)
    elif n.key > r.key:     # 삽입할 노드의 키가 루트보다 크면
        if r.right is None: # 루트의 오른쪽 자식이 없으면
            r.right = n     # n은 루트의 오른족 자식이 됨
            return True     
        else:          			 # 루트의 오른쪽 자식이 있으면
            return insert_bst(r.right, n)   # 오른쪽 자식에게 삽입하도록 함(순환)
    else:           			 # 키가 중복되면
        return False      		  # 삽입하지 않음

 

* 삭제 연산

• 삭제할 노드의 종류에 따라 3가지 경우로 구분된다.

 

▶case1: 단말 노드의 삭제(가장 간단)

#case 1: 단말노드의 삭제
def delete_bst_case1 (parent, node, root) :
    if parent is None: 			# 삭제할 단말 노드가 루트이면
        root = None			# 공백 트리가 됨
    else :
        if parent.left == node : 	# 삭제할 노드가 부모의 왼쪽 자식이면
            parent.left = None		# 부모의 왼쪽 링크를 None
        else :				# 오른쪽 자식이면
            parent.right = None		# 부모의 오른쪽 링크를 None

    return root			        # root가 변경될 수도 있으므로 반환

 

▶case 2: 자식이 하나인 노드의 삭제

# case2 : 자식이 하나인 노드의 삭제
def delete_bst_case2 (parent, node, root) :
    if node.left is not None :		# 삭제할 노드가 왼쪽 자식만 가짐
        child = node.left		# child는 왼쪽 자식
    else :				# 삭제할 노드가 오른쪽 자식만 가짐
        child = node.right		# child는 오른쪽 자식

    if node == root :			# 없애려는 노드가 루트이면
        root = child			# 이제 child가 새로운 루트가 됨
    else :
        if node is parent.left : 	# 삭제할 노드가 부모의 왼쪽 자식
            parent.left = child		# 부모의 왼쪽 링크를 변경
        else :			        # 삭제할 노드가 부모의 오른쪽 자식
            parent.right = child	# 부모의 오른쪽 링크를 변경

    return root				# root가 변경될 수도 있으므로 반환

 

▶case 3: 두 개의 자식을 모두 갖는 노드의 삭제(가장 복잡)

• 삭제할 노드를 실제로 삭제하지 않고 노드의 내용만을 적절한 "후계자(successor)"의 내용으로 교체하는 방법
• 후계자 노드는 삭제할 노드와 키값이 비슷한 노드이다.
• 후계자로서, 왼쪽 서브트리의 가장 큰 값(12)이나 오른쪽 서브트리의 가장 작은 값(22)을 가진 노드가 적절하다.

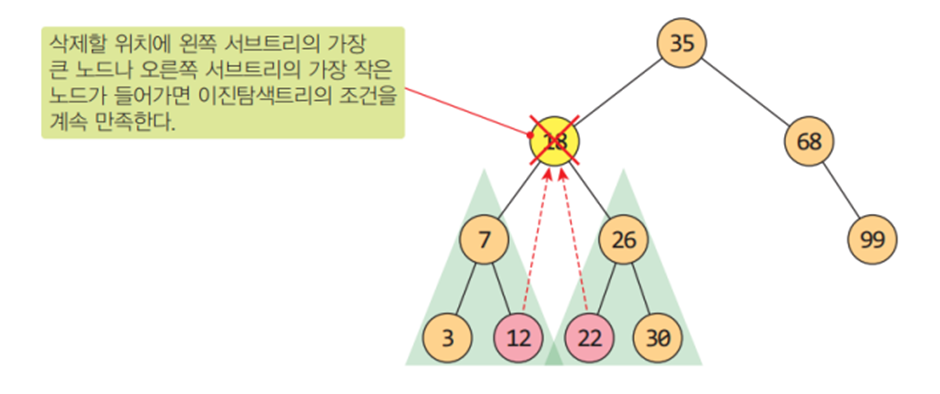
< 후계자 노드의 선택 > 출처 : 파이썬으로 쉽게 풀어쓴 자료구조

 - 후계자 노드 탐색 방법

• 왼쪽 서브트리에서 가장 큰 값은 왼쪽 서브트리의 가장 오른쪽에 있는 노드이고,
• 오른쪽 서브트리에서 가장 작은 값은 오른쪽 서브트리의 가장 왼쪽에 있는 노드이다.
• 두 개의 후계자 중 어떤 것을 선택해도 괜찮다.
• 앞서 설명한 최대/최소 키 탐색 방법을 사용한다.

1. 삭제할 노드의 후계자(succ, 22)와 그의 부모노드(succp, 26)를 찾는다.
2. 후계자의 자식을 후계자 부모의 자식으로 연결한다.
3. 후계자(succ)의 데이터(키와 값)를 모두 삭제할 노드(node, 18)에 복사한다.

 

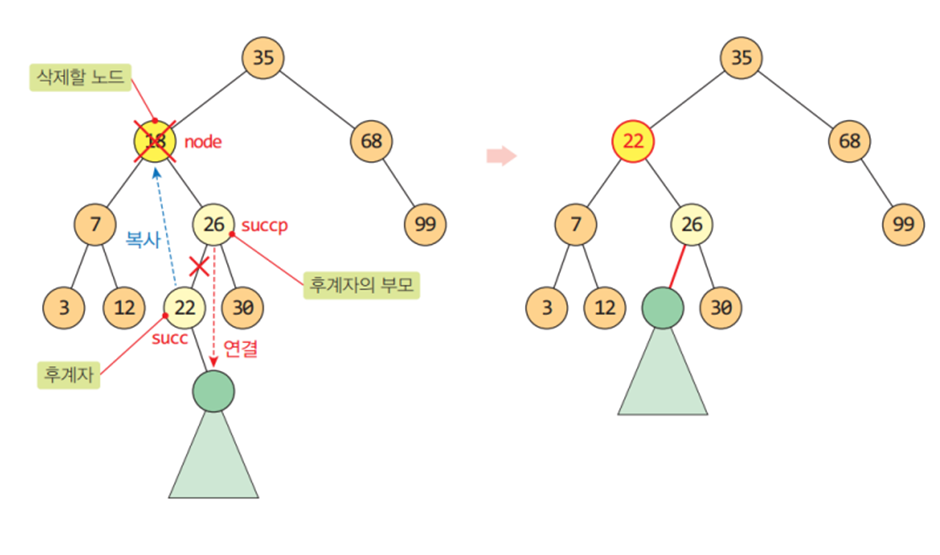
# case3 : 두 개의 자식을 모두 갖는 노드의 삭제 ( 후보자 = 오른쪽 서브트리의 최소 키)

def delete_bst_case3 (parent, node, root) :	
# parent는 여기서 쓰이지 않지만 앞선 delete_bst_case의 삭제 연산들과의 일관성을 위해 삭제하지 않고 넣음

    succp = node		        # 후계자의 부모 노드(succp)를 node로 초기화
    succ = node.right		    	# 후계자 노드(succ)를 node.right로 초기화
    while (succ.left != None) :		# 후계자와 부모노드 탐색에 최소 키 탐색 방법 적용
        succp = succ				
        succ = succ.left

    if (succp.left == succ) :		# 후계자가 왼쪽 자식이면
        succp.left = succ.right		# 후계자의 오른쪽 자식을 후계자의 부모에 연결
    else :			        # 후계자가 오른쪽 자식이면(후계자가 왼쪽 자식을 가지고 있지 않은 경우)
        succp.right = succ.right	# 후계자의 오른쪽 자식을 후계자의 부모에 연결

    node.key = succ.key	    		# 후계자의 키와 값을
    node.value= succ.value	    	# 삭제할 노드에 복사

    return root				# 일관성을 위해 root 반환

 

▶모든 경우에 대한 삭제연산

• 먼저 삭제할 노드 node와 부모 노드 parent를 찾아야 한다.

# 이진탐색트리 삭제연산(노드를 삭제함)
def delete_bst (root, key) :
    if root == None : return None       		# 공백 트리

    parent = None                       		# 삭제할 노드의 부모 변수 초기화
    node = root                         	   	# 삭제할 노드 변수 root로 초기화 
    while node != None and node.key != key :		# parent 탐색
        parent = node
        if key < node.key : node = node.left
        else : node = node.right

    if node == None : return None       		# 삭제할 노드를 못 찾는 경우 
    if node.left == None and node.right == None:	# case 1: 단말 노드 삭제
        root = delete_bst_case1 (parent, node, root)
    elif node.left==None or node.right==None :		# case 2: 유일한 자식
        root = delete_bst_case2 (parent, node, root)
    else :						# case 3: 두 개의 자식
        root = delete_bst_case3 (parent, node, root)

 

* 이진탐색트리의 성능 분석

• 좌우의 서브 트리가 균형을 이루고 있는 경우에는 O(log_2 n)이고,
• 한쪽으로 치우치는 완전한 경사 이진트리일 경우에는 트리의 높이 h가 n과 같아진다.

균형이진트리와 경사이진트리의 높이

• 이진탐색트리의 효율을 높이기 위해서는 가능한 한 트리가 좌우로 균형 잡히게 만들어야 한다.
• 이진탐색트리의 높이를 log_2 n으로 한정시키는 균형기법에는 AVL트리가 있다.

이진탐색트리 각 연산의 최선과 최악의 경우에 대한 시간복잡도