[Python 자료구조 #탐색트리3] AVL트리, AVL트리를 이용한 맵

* 심화 학습 : 균형이진탐색트리 - AVL 트리

• AVL 트리는 Adelson-Velskii와 Landis에 의해 제안된 트리이다. AVL트리는 항상 균형 트리를 보장하기 때문에 탐색과 삽입, 삭제 연산에서 항상 O(log_2 n)의 처리시간을 보장한다.
• AVL 트리를 정의하기 위해서는 균형인수를 정의해야 한다.
• 어떤 노드의 균형 인수(balance factor)는 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차로 정의된다.
• AVL 트리는 비균형 상태가 되면 스스로 노드들을 재배치하여 균형 상태로 만든다.

AVL 트리 정의
AVL 트리는 모든 노드에서 왼쪽 서브트리와 오른쪽 서브트리의 높이 차가 1을 넘지 않는 이진탐색 트리이다. 즉 모든 노드의 균형 인수는 0이나 ±1이 되어야 한다.

AVL 트리와 비 AVL 트리

 

* AVL 트리의 삽입 연산

• 노드가 삽입되면 삽입되는 위치에서 루트까지의 경로에 있는 모든 조상 노드들의 균형 인수가 영향을 받는다.
• 균형이 깨진 트리의 서브 트리를 회전시켜 다시 균형을 잡을 수 있다.

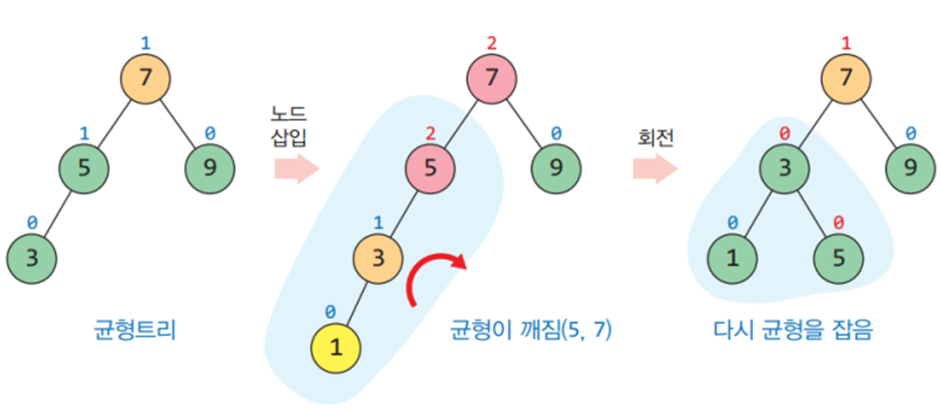
삽입 연산에서 균형이 깨지는 경우는 다음과 같이 4가지가 있다.

(새로 삽입된 노드 N으로부터 가장 가까우면서 균형 인수가 ±2가 된 조상 노드를 A라고 하자)

• LL 타입 : N이 A의 왼쪽 자식의 왼쪽 서브 트리에 삽입된다.
• LR 타입 : N이 A의 왼쪽 자식의 오른쪽 서브 트리에 삽입된다.
• RR 타입 : N이 A의 오른쪽 자식의 오른쪽 서브 트리에 삽입된다.
• RL 타입 : N이 A의 오른족 자식의 왼쪽 서브 트리에 삽입된다.

 

LL과 RR 회전은 한번만 회전하는 단순 회전(single rotation) 방법이다. 

LR과 RL은 두 번의 회전이 필요한 이중 회전(double rotation)이다.

 

1. LL 회전

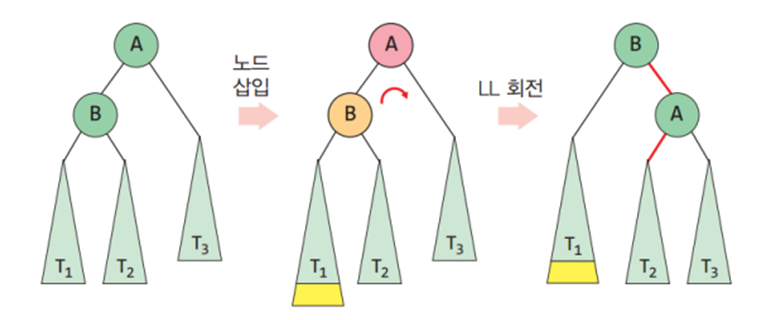
일반적인 경우의 LL 회전

# LL 회전
# 회전에 의해 루트가 변경되므로 반드시 새로운 루트를 반환해야 하는 것에 유의할 것
def rotateLL(A) :			# 시계방향 회전
	B = A.left			# A의 왼쪽서브트리를 담을 B 변수 선언
	A.left = B.right
	B.right = A
	return B			# 새로운 루트 B를 반환

 

2. RR회전

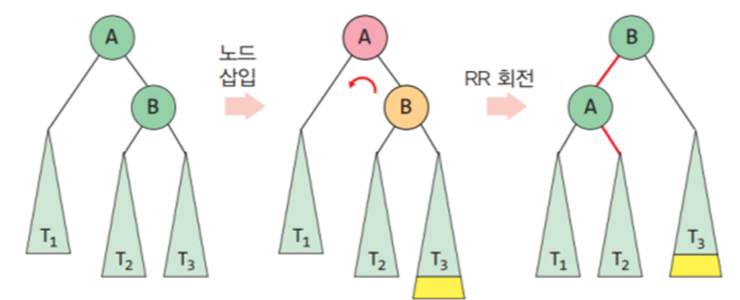
일반적인 경우의 RR 회전

# RR회전
def rotateRR(A) :			# 반시계방향 회전
	B = A.right			# A의 오른쪽 서브트리를 담을 새로운 변수 B 선언
	A.right = B.left
	B.left = A
	return B			# 새로운 루트 B를 반환

 

3. RL회전

일반적인 경우의 RL 회전

# RL 회전
def rotateRL(A) :
	B = A.right
	A.right = rotateLL(B)		# LL 회전
	return rotateRR(A)		# RR 회전

 

4. LR회전

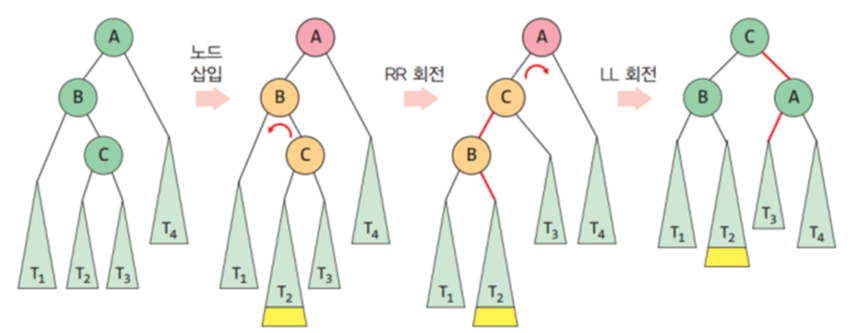
일반적인 경우의 LR회전

# LR회전
def rotateLR(A) :
	B = A.left
	A.left = rotateRR(B)		# RR회전
	return rotateLL(A)		# LL회전

 

▶재균형 함수

노드의 균형을 검사하여 균형이 깨져 있으면 재균형하는 전체 함수는 다음과 같다.

↓calc_height() 함수 참고(이전 포스팅에서 다룸)

def calc_height(n) :

    if n is None :          # 공백 트리 -> 0을 반환                

        return 0

    hLeft = calc_height(n.left)     # 왼쪽 트리의 높이 -> hLeft

    hRight = calc_height(n.right)   # 오른쪽 트리의 높이 -> hRight

    if (hLeft > hRight) :       # 더 높은 높이에 1을 더해 반환.

        return hLeft + 1

    else:

        return hRight + 1

# 재균형 함수
def calc_height_diff(n) :			# 균형인수 계산기
    if n==None :
       return 0
    return calc_height(n.left) - calc_height(n.right)
    
def reBalance (parent) :
	hDiff = calc_height_diff(parent)	# parent의 왼쪽과 오른쪽 서브트리 높이 차를
						# 반환하는 함수. parent가 None이면 0을 반환
	if hDiff > 1 :
		if calc_height_diff( parent.left ) > 0 :
			parent = rotateLL( parent )
		else :
			parent = rotateLR( parent )
	elif hDiff < -1 :
		if calc_height_diff( parent.right ) < 0 :
			parent = rotateRR( parent )
		else :
			parent = rotateRL( parent )
	return parent

 

▶삽입 함수 구현

이진탐색트리의 삽입함수와 유사하지만 두 가지 차이가 있다.

• 삽입이 끝나면 반드시 재균형 함수를 호출해서 균형을 확인해야 한다.
• 이진탐색트리에서와 달리 삽입 후 서브트리의 루트노드가 변경되는 경우가 많다. 따라서 루트를 반환해야 한다.

# AVL트리의 삽입 연산 
# 이진탐색트리ADT에서 삽입할 node의 parent를 찾는 함수를 통해 parent를 찾아서 인수로 넣는다.
def insert_avl(parent, node) :		 
    if node.key < parent.key :		# 노드의 키가 부모 노드의 키보다 작을 경우
        if parent.left != None :	# 부모 노드의 왼족 서브트리가 비어있지 않으면
            parent.left = insert_avl(parent.left, node)	# AVL 트리 삽입 연산 순환 호출 
        else :				# 부모 노드의 왼쪽 서브트리가 비어있으면 바로 삽입
            parent.left = node
        return reBalance(parent)	# 재균형 함수를 거치고 반환된 새로운 루트를 반환한다.

    elif node.key > parent.key :	# 노드의 키가 부모 노드의 키보다 클 경우
        if parent.right != None :
            parent.right = insert_avl(parent.right, node)
        else :
            parent.right = node
        return reBalance(parent)
    else :				# 노드의 키가 부모 노드의 키와 같을 경우 에러 메시지 반환
        print("중복된 키 에러")

 

* AVL 트리 구축의 예

다음과 같은 데이터가 순서대로 주어졌을 때 AVL 트리가 만들어지는 과정

[7, 8, 9 , 2, 1, 5, 3, 6, 4]

 

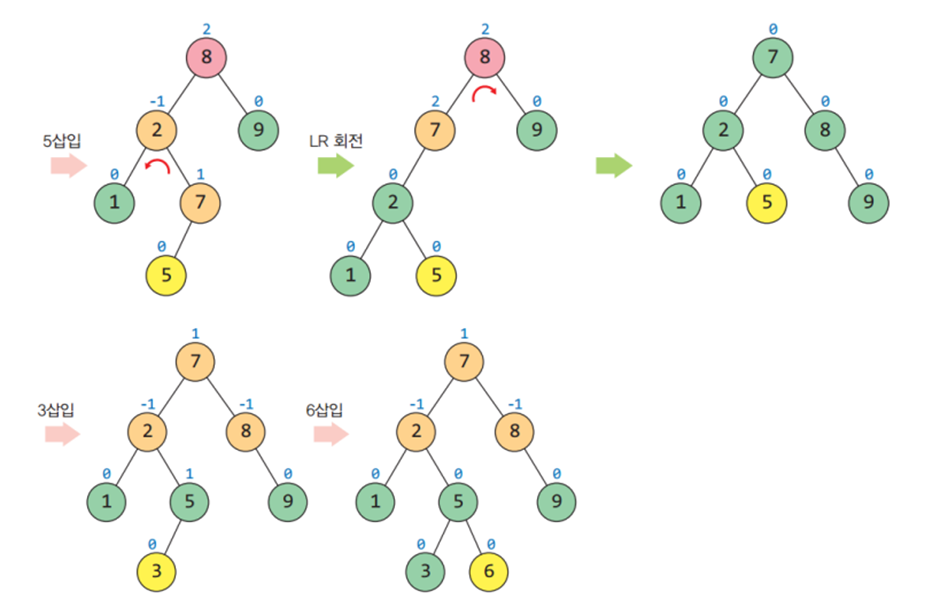
* AVL 트리를 이용한 맵

이전 포스팅에서 구현한 BSTMap에 새로운 삽입기능만 추가한다.(클래스 상속기능 사용)

↓levelorder(), count_leaf(), calc_height(), calc_height_diff() 코드 참고(CircularQueue()는 원형큐 포스팅 참고)

def levelorder(root):       # 레벨 순회 함수

    queue = CircularQueue()

    queue.enqueue(root)

    while not queue.isEmpty():

        n = queue.dequeue()

        if n is not None:

            print(n.key, end=" ")

            queue.enqueue(n.left)

            queue.enqueue(n.right)

def count_leaf(n):  # 단말노드 개수 세는 함수

    if n is None:

        return 0

    elif n.left is None and n.right is None:

        return 1

    else:

        return count_leaf(n.left) + count_leaf(n.right)

def calc_height(n):     # 이진트리 높이 계산

    if n is None:  # 공백 트리 -> 0을 반환

        return 0

    hLeft = calc_height(n.left)  # 왼쪽 트리의 높이 -> hLeft

    hRight = calc_height(n.right)  # 오른쪽 트리의 높이 -> hRight

    if hLeft > hRight:  # 더 높은 높이에 1을 더해 반환.

        return hLeft + 1

    else:

        return hRight + 1

def calc_height_diff(n):        # 균형인수 계산

    if n == None:

        return 0

    return calc_height(n.left) - calc_height(n.right)

from BSTMap import*		# BSTMap.py에서 정의한 모든 것을 사용함

class AVLMap(BSTMap):		# BSTMap클래스를 상속한 AVLMap 클래스 선언
    def __init__ (self):	# AVLMap 클래스의 생성자 함수
        super().__init__()	# 부모(BSTMap) 클래스의 생성자 호출

    def insert(self, key, value=None):	# AVL 트리의 삽입 연산을 다시 구현(재정의.overriding)
        n = BSTNode(key, value)
        if self.isEmpty() :
           self.root = n
        else :
           self.root = insert_avl(self.root, n)

# display연산도 overriding
# 결과를 앞에서 살펴본 AVL 트리 구축 예와 비교하기 위해 중위순회가 아니라 레벨 순회를 사용.
    def display(self, msg = 'AVLMap :'):	
        print(msg, end='')
        levelorder(self.root)
        print()

node = [7,8,9,2,1,5,3,6,4]
map = AVLMap()

for i in node :
    map.insert(i)
    map.display("AVL(%d): "%i)

print(" 노드의 개수 = %d" % count_node( map.root ))
print(" 단말의 개수 = %d" % count_leaf( map.root ))
print(" 트리의 높이 = %d" % calc_height( map.root ))
---------------------------------------------------------
AVL(7): 7
AVL(8): 7 8
AVL(9): 8 7 9
AVL(2): 8 7 9 2
AVL(1): 8 2 9 1 7
AVL(5): 7 2 8 1 5 9
AVL(3): 7 2 8 1 5 9 3
AVL(6): 7 2 8 1 5 9 3 6
AVL(4): 7 3 8 2 5 9 1 4 6
 노드의 개수 = 9
 단말의 개수 = 4
 트리의 높이 = 4