-
[Python 자료구조 #그래프3] 신장 트리Programming 기초/Python 2023. 5. 27. 20:13
* 신장 트리(spanning tree)
- 그래프내의 모든 정점을 포함하는 트리이다.
- 트리의 일종이므로 모든 정점들이 연결되어 있고 사이클이 없어야 하고, 그래프의 n개의 정점을 정확히 (n-1)개의 간선으로 연결해야 한다.
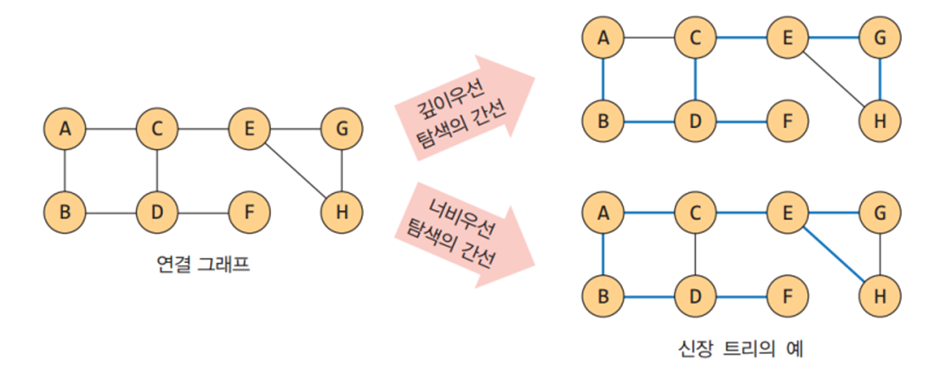
- 하나의 같은 그래프에 다양한 신장 트리가 가능하다.
- 신장 트리는 깊이우선이나 너비우선 탐색 도중에 사용된 간선들만 모으면 된다.
# 너비우선탐색 함수 bfs를 수정한 코드 # 탐색 도중에 추가되는 간선을 순서대로 출력한 코드 import collections def bfsST(graph, start): visited = set([start]) # 맨 처음에는 start만 방문한 정점임 queue = collections.deque([start]) # 파이썬 컬렉션의 덱 생성(큐로 사용) while queue: # 공백이 아닐 때까지 v = queue.popleft() # 큐에서 하나의 정점 v를 빼냄 nbr = graph[v] - visited # nbr = {v의 인접정점} - {방문정점} for u in nbr: # 갈 수 있는 모든 인접 정점에 대해 print("(", v, ",", u, ") ", end="") # (v, u)간선 추가 visited.add(u) # 이제 u는 방문했음 queue.append(u) # u를 큐에 삽입 # 위의 그래프에 대한 신장트리를 출력하는 코드이다. mygraph = { "A": set(["B", "C"]), "B": set(["A", "D"]), "C": set(["A", "D", "E"]), "D": set(["B", "C", "F"]), "E": set(["C", "G", "H"]), "F": set(["D"]), "G": set(["E", "H"]), "H": set(["E", "G"]), } bfsST(mygraph, "A") print() ---------------------------------------------------- ( A , B ) ( A , C ) ( B , D ) ( C , E ) ( D , F ) ( E , G ) ( E , H )* 위상 정렬(topological sort)
- 방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것을 방향 그래프의 위상정렬이라고 한다.
- 선행 : 방향 그래프에서 간선 <u, v>가 있다면 "정점 u는 정점 v를 선행한다"고 말한다.
- 위상 정렬을 위해서는 방향 그래프에 사이클이 존재하지 않아야 한다.

출처 : 파이썬으로 쉽게 풀어쓴 자료구조 ▶ 위상 정렬 알고리즘
- 진입 차수가 0인 정점(선행 정점이 없는 정점)을 선택한다.
- 선택된 정점과 여기에 부착된 모든 간선을 삭제한다.
- 이때 간선이 삭제되므로 삭제되는 간선과 연결된 남아있는 정점들의 진입차수도 변경되어야 한다.
- 이 과정을 반복하여 모든 정점이 삭제되면 알고리즘이 종료
- 전체 과정에서 정점이 삭제되는 순서가 위상 순서(topological order)가 된다.
- 만약 진입 차수 0인 정점이 여러 개 있다면 어느 정점을 선택해도 된다.
- 하지만 진입 차수 0인 정점이 없다면 위상 정렬은 불가능하다. (이것은 그래프에 사이클이 존재하는 것을 말한다.)

위상 정렬 과정의 예 : B-E-A-C-D-F ▶ 위상 정렬 알고리즘 구현
- 이번에는 인접행렬로 표현한 그래프를 이용
- 각 정점의 진입 차수를 기록. (진입차수는 리스트를 이용)
- 진입차수가 0인 정점들은 따로 관리하기 위해 리스트 vlist를 사용. 처음에는 inDeg에서 진입차수가 0인 정점들을 모두 찾아 vlist에 추가한다.
- vlist가 공백이 아니면 하나의 정점 v를 꺼내 출력하고 v에 인접한 정점들의 inDeg를 1씩 줄인다. 진입차수가 0으로 줄어든 정점은 vlist에 추가. 이 과정을 vlist가 공백이 될 때까지 반복.
def topological_sort_AM(vertex, graph): n = len(vertex) inDeg = [0] * n # 정점의 진입차수 저장. in-degree(진입 차수). # inDeg = [0,0,0,0,0..] n개 만큼 요소 생성 for i in range(n): # i = 0 ~ n-1 for j in range(n): # j = 0 ~ n-1 if graph[i][j] > 0: # 간선이 있으면 inDeg[j] += 1 # 진입 차수를 1 증가시킴 # inDeg = [0]에 A정점의 진입 차수가 저장. [3]에 D정점의 진입 차수 저장됨 vlist = [] # 진입 차수가 0인 정점에 가리키는 인덱스를 담을 리스트 생성 for i in range(n): if inDeg[i] == 0: vlist.append(i) while len(vlist) > 0: v = vlist.pop() print(vertex[v], end=" ") # 진입차수가 0인 정점들을 화면에 출력 for u in range(n): # u = 0 ~ n-1 if v != u and graph[v][u] > 0: # 대각선 성분이 아니고 진입차수가 1이상이면 inDeg[u] -= 1 # 연결된 정점의 진입차수 감소 if inDeg[u] == 0: # 진입차수가 0이면 vlist.append(u) # vlist에 추가vertex = ["A", "B", "C", "D", "E", "F"] graphAM = [ [0, 0, 1, 1, 0, 0], [0, 0, 0, 1, 1, 0], [0, 0, 0, 1, 0, 1], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0], ] print("topological_sort: ") topological_sort_AM(vertex, graphAM) print() ----------------------------------------- topological_sort: B E A C D F'Programming 기초 > Python' 카테고리의 다른 글
[Python 자료구조 #가중치 그래프2] 최소비용 신장 트리 - Kruskal의 MST 알고리즘, Prim의 MST 알고리즘 (0) 2023.05.29 [Python 자료구조 #가중치 그래프1] 인접행렬/인접리스트를 이용한 가중치 그래프 표현 (0) 2023.05.27 [Python 자료구조 #그래프2] 그래프의 탐색(DFS, BFS), 연결 성분 검사 (0) 2023.05.27 [Python 자료구조 #탐색트리3] AVL트리, AVL트리를 이용한 맵 (0) 2023.05.26 [Python 자료구조 #탐색트리2] 이진탐색트리를 이용한 맵 (0) 2023.05.26