[Python 자료구조 #가중치 그래프2] 최소비용 신장 트리 - Kruskal의 MST 알고리즘, Prim의 MST 알고리즘

* 최소비용 신장 트리(MST: minimum spanning tree)

• 통신망 도로망 유통망 등은 대개 길이, 구축비용, 전송 시간 등의 가중치를 간선에 할당한 가중치 그래프로 표현할 수 있다.
• 이러한 망을 가장 적은 비용으로 구축하는 문제를 생각해 보자. 조건은 다음과 같다.

1. 그래프의 모든 정점들은 연결되어야 한다.
2. 연결에 필요한 간선의 가중치 합(비용)이 최소가 되어야 한다.
3. 사이클은 두 정점을 연결하는 두 가지 경로를 제공하므로 비용 측면에서 바람직하지 않다. 따라서 사이클이 없이 (n-1)개의 간선만을 사용해야 한다.

→ 결과적으로 '신장 트리'

 

• 최소비용 신장 트리는 그래프의 여러 가능한 신장 트리들 중에서 사용된 간선들의 가중치 합이 최소인 신장 트리를 말한다.
• 최소비용 신장 트리를 구하는 방법에는 Kruskal과 Prim의 알고리즘이 있다.

 

* Kruskal의 MST 알고리즘

• Kruskal의 알고리즘은 탐욕적인 방법(greedy method)이라는 알고리즘 설계에서 중요한 기법 중의 하나를 사용한다.
• Kruskal의 알고리즘의 시간 복잡도는 간선들을 정렬하는 시간에 좌우된다. 따라서 퀵 정렬이나 최소 힙과 같은 효율적인 정렬 알고리즘을 사용한다면 시간 복잡도는 (elog_2 e)이다. e는 간선의 개수이다.

탐욕적인 방법 (greedy method): 
어떤 결정을 해야 할 때마다 "그 순간에 최적"이라고 생각되는 것을 선택하는 방법이다. 순간의 최적이라고 판단했던 선택을 모아 최종적인 답을 만들었을 때 이것이 "궁극적으로 최적"이라는 보장은 없다. 탐욕적인 방법은 항상 최적의 해답을 주는지를 반드시 검증해야 한다. Kruskal의 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다. 

• Kruskaldml 알고리즘은 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택한다. 이러한 과정을 반복하여 그래프의 모든 정점을 최소비용으로 연결하는 최적 해답을 구한다.

Kruskal의 최소 비용 신장 트리 알고리즘
kruskal()
1. 그래프의 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
2. 가장 가중치가 작은 간선 e를 뽑는다.
3. e를 신장 트리에 넣었을 때 사이클이 생기면 넣지 않고 2번으로 이동한다.
4. 사이클이 생기지 않으면 최소 신장 트리에 삽입한다.
5. n-1개의 간선이 삽입될 때까지 2번으로 이동한다.

 

▶ 추가할 간선에 대한 사이클 검사

• Union-Find는 서로소(disjoint)인 집합들을 표현할 때 사용하는 독특한 형태의 집합 자료구조.
• union(x, y)은 원소 x와 y가 속해있는 집합을 입력으로 받아 이들의 합집합을 만드는 연산
• find(x) 연산은 여러 집합들 중에서 원소 x가 속해있는 집합을 반환하는 연산이다.

parent = []     				# 각 노드의 부모노드 인덱스를 담는 리스트 생성
set_size = 0    				# 전체 집합의 개수를 담는 변수 생성

• 그래프의 모든 정점에 대해 부모 노드의 인덱스를 저장하기 위해 parent 리스트와 현재 집합의 개수를 나타내는 set_size를 전역변수로 사용한다.

# 집합의 초기화 함수
def init_set(nSets) :			
    global set_size, parent 		# 전역변수 사용(변경)을 위함
    set_size = nSets;			# 집합의 개수
    for i in range(nSets):		# 모든 집합에 대해
        parent.append(-1)		# 각각이 고유의 집합(부모가 -1인 노드는 루트노드를 뜻함)

# 정점 id가 속한 집합을 찾는 함수인데, 실제로는 집합을 반환하는 것이 아닌,
# id가 속한 트리(집합)의 루트노드 인덱스를 반환하는 함수로 구현.
def find(id) :			# 정점 id가 속한 집합의 대표번호 탐색
    while (parent[id] >= 0) :	# 부모가 있는 동안(-1이 아닌 동안)
        id = parent[id]		# id를 부모 id로 갱신
    return id			# 최종 id반환. 트리의 맨 위 노드의 id임

# 두 집합을 병합(s1을 s2에 병합시킴)
def union(s1, s2) :				
    global set_size		# 전역변수 사용(변경)을 위해 global 선언
    parent[s1] = s2		# s1을 s2에 병합시킴
    set_size = set_size - 1	# 집합의 개수가 줄어 듦

• union(s1, s2)의 s1과 s2는 정점의 인덱스를 의미한다.
• s1을 s2에 병합시키고 있지만 s2을 s1에 병합시켜도 결과는 같다. (단지, find()함수 내의 반복문의 반복횟수가 다름.)

파이썬에서 집합(set) 클래스를 제공하지만 여기서는 사용하지 않음. set은 집합 하나와 관련된 클래스이고, 따라서 여러 집합이 있을 때 어떤 원소가 속한 집합을 찾는 find와 같이 연산은 제공하지 않기 때문이다.
파이썬의 set을 사용하고 find 함수를 추가할 수는 있다. 이 연산은 어떤 원소 e가 포함된 집합을 찾기 위해 모든 집합에 대해 in 연산을 처리해야 할 것이다. 이보다는 위의 코드가 훨씬 효율적이다.

 

# kruskal의 최소 비용 신장 트리 프로그램
def MSTKruskal(vertex, adj):			  # 매개변수: 정점리스트, 인접행렬
    vsize = len(vertex)        		  	  # 정점의 개수
    init_set(vsize)             		  # 정점 집합 초기화
    eList = []                   		  # 간선 리스트

# 인접 행렬을 (i, j, weight)의 튜플로 바꿔서 elist 리스트에 저장함
    for i in range(vsize) :     		  # 모든 간선을 리스트에 넣음
        for j in range(i+1, vsize) :	# 삼각 영역만
            if adj[i][j] != None :
                eList.append( (i,j,adj[i][j]) )	# 튜플로 저장

# 간선 리스트를 가중치의 내림차순으로 정렬: 람다 함수 사용
# 내림 차순은 sort() 메소드의 매개변수 reverse를 이용해 처리할 수 있다.
# sort()에 reverse = tree, 키워드 인수를 넣는다.
# weight의 순으로 정렬하기 위해 lambda 함수를 사용한다.
# 내림차순인 이유는 pop은 마지막 요소를 제거하는 함수이기 때문에 마지막튜플의 weight가 가장 작아야한다.

    eList.sort(key= lambda e : e[2], reverse=True)

    edgeAccepted = 0
    while (edgeAccepted < vsize - 1) :		# 정점 수 -1개의 간선
        e = eList.pop(-1)       		# 가장 작은 가중치를 가진 간선 e = (u, v, weight)
        uset = find(e[0])      			# 두 정점이 속한 집합 번호 uset = find(i)
        vset = find(e[1])			# vset = find(j)

        if uset != vset :       		# 두 정점이 다른 집합의 원소이면
            print("간선 추가 : (%s, %s, %d)" % (vertex[e[0]], vertex[e[1]], e[2])) # 간선추가 출력
            union(uset, vset)   		# 두 집합을 합함
            edgeAccepted += 1			# 간선이 하나 추가됨

↓람다 함수 설명

람다 함수는 이름이 없는 한 줄짜리 함수로 간단한 함수를 만들어 인수로 넘겨줄 때 매우 유용. 

형식 -> lamda 인자(argument) : 식(expression)

람다 함수는 보통 함수로 저장하지 않고 바로 사용한다. 다음은 두 수를 곱하는 간단한 연산을 람다함수로 구현하고, 이를 바로 사용한 예이다.

 

print((lambda x, y : x*y)(3,4))          # 12 출력. 3과 4가 x와 y에 각각 대응됨

람다 함수는 중요하므로 잘 알아두는 것이 좋다.

 

앞의 코드에서 정렬을 위해 람다 함수를 사용했는데 다음과 같이 해석한다.

lambda e : e[2] 

# 예를 들어, e가 (2, 3, 17)이면 17을 반환

 

* Prim의 MST 알고리즘

• 하나의 정점에서부터 시작하여 트리를 단계적으로 확장해나가는 방법이다. 
• Kruskal의 알고리즘은 간선을 기반으로 하는데 비해 Prim의 알고리즘은 정점을 기반으로 한다.
• Prim의 알고리즘은 주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복하므로 O(n^2)의 시간 복잡도를 갖는다.
• Kruskal의 알고리즘은 복잡도가 O(e log_2 e)이므로 정점의 개수에 비해 간선의 개수가 매우 적은 희박한 그래프(sparse graph)를 대상으로 할 경우에는 Krsuskal의 알고리즘이 적합하고, 반대로 완전 그래프와 같이 간선이 매우 많은 그래프의 경우에는 Prim의 알고리즘이 유리하다.

prim()
1. 그래프에서 시작 정점을 선택하여 초기 트리를 만든다.
2. 현재 트리의 정점들(초록색으로 칠해진 모든 정점들)과 인접한 정점들 중에서 간선의 가중치가 가장 작은 정점 v를 선택한다.
3. 이 정점 v와 이때의 간선을 트리에 추가한다.
4. 모든 정점이 삽입될 때까지 2번으로 이동한다.

 

▶ 현재의 MST에 인접한 정점들 중에서 가장 가까운(간선의 가중치가 작은) 정점을 찾는 함수

INF = 9999
# 현재 트리에 인접한 정점들 중에서 가장 가까운 정점을 찾는 함수
# dist 는 현재 트리(이미 선택된 모든 정점들)를 기준으로 최소가중치의 후보를 담고있는 리스트
# selected는 MST에 이미 선택된(MST에 포함된) 정점들을 담고 있는 리스트이다.
def getMinVertex(dist, selected):
    minv = 0
    mindist = INF
    for v in range(len(dist)):				# 모든 정점들에 대해
        if not selected[v] and dist[v] < mindist:	# 선택 안 되었던 정점이고
            mindist = dist[v]				# 가중치가 작으면
            minv = v					# miv 갱신
    return minv						# 최소 가중치의 정점의 인덱스를 반환

위에서 무한대를 충분히 큰 값 9999를 사용하였다.
무한대를 나타내기 위해 파이썬에서 가장 큰 정수 값을 사용할 수도 있다. sys 모듈의 maxsize를 사용하는 것이다. 
import sys
INF = sys.maxsize               # 가장 큰 가중치 (정수 무한대)

만약 무한대의 실수 값을 원한다면 다음과 같은 코드를 사용하면 된다.
INF = float('Inf')                    # 가장 큰 가중치 ( 실수 무한대)

#Prim의 최소 비용 신장 트리 프로그램
# 시작 정점을 미리 정해놔야 한다. 여기선 A가 시작정점으로 고정되어있다.
def MSTPrim(vertex, adj):
    vsize = len(vertex) 
    dist = [INF] * vsize			# dist: [INF, INF, ... INF]
    selected = [False] * vsize			# selected: [False, False, ... False]
    dist[0] = 0					# dist : [0, INF, ...INF] A 정점을 시작정점으로 고정.

    for i in range(vsize):			# 정점의 수만큼 반복
        u = getMinVertex(dist, selected)	# u는 현재 트리에서 가장 가까운 정점의 인덱스
        selected[u] = True			# u는 이제 선택됨
        print(vertex[u], end=" ")		# u를 출력

# 내부 루프 현재 트리(이미 지나온 모든 정점들)에서 연결된 정점 중 선택되지 않은 정점의 가중치를 담는 과정.
# dist의 값을 바꿈.
        for v in range(vsize):		
            if adj[u][v] != None:					# (u, v) 간선이 있으면 dist[v] 갱신
                if selected[v] == False and adj[u][v] < dist[v]:	# 이미 선택된 정점이 아니고 
                    dist[v] = adj[u][v]
    print()

1. 위 그래프에 Prim의 MST 알고리즘을 적용하는 예시.

vertex = ["A", "B", "C", "D", "E", "F", "G"]
weight = [
    [None, 29, None, None, None, 10, None],
    [29, None, 16, None, None, None, 15],
    [None, 16, None, 12, None, None, None],
    [None, None, 12, None, 22, None, 18],
    [None, None, None, 22, None, 27, 25],
    [10, None, None, None, 27, None, None],
    [None, 15, None, 18, 25, None, None],
]

print("MST By Prim's Algorithm")
MSTPrim(vertex, weight)
-------------------------------------------
MST By Prim's Algorithm
A F E D C B G

 

2. 아래 그래프는 위 그래프에서 (F, E) 값만 30으로 변경되었다. 아래 그래프에 Prim의 MST 알고리즘을 적용해보자.

(아래 그림에서 실수로 (A,B) 간선의 가중치 29를 28로 잘못 기입했다.)

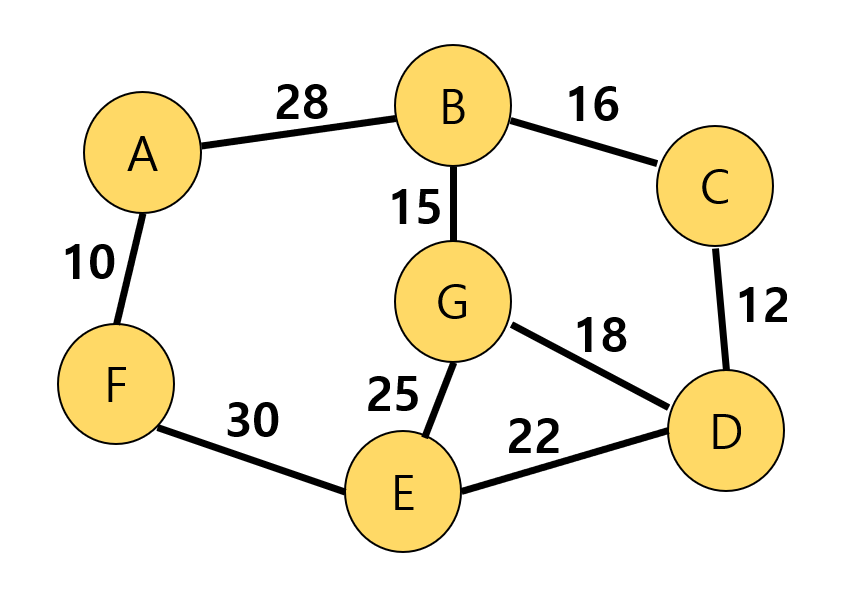
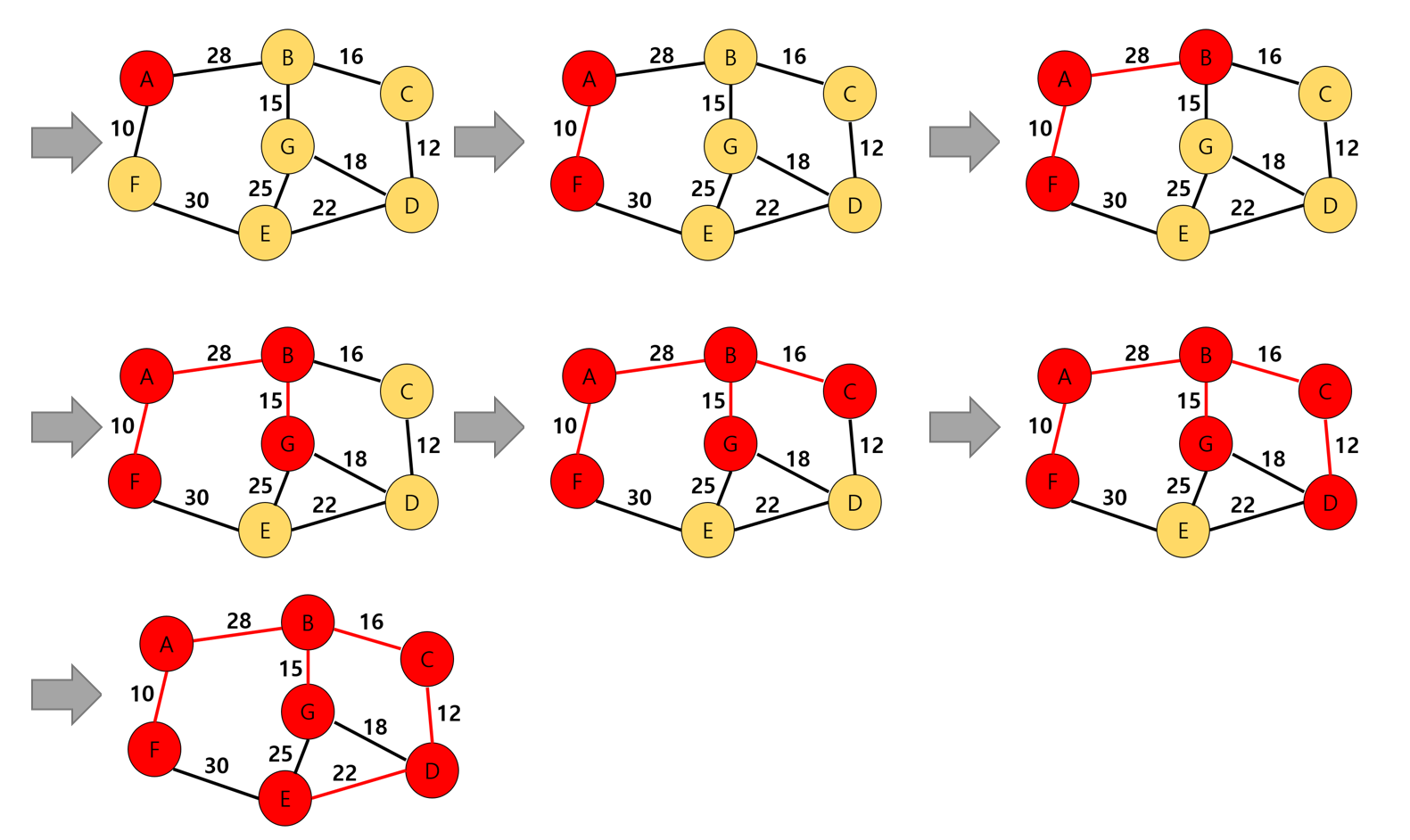
vertex = ["A", "B", "C", "D", "E", "F", "G"]
weight = [
    [None, 29, None, None, None, 10, None],
    [29, None, 16, None, None, None, 15],
    [None, 16, None, 12, None, None, None],
    [None, None, 12, None, 22, None, 18],
    [None, None, None, 22, None, 30, 25],
    [10, None, None, None, 30, None, None],
    [None, 15, None, 18, 25, None, None],
]

print("MST By Prim's Algorithm")
MSTPrim(vertex, weight)
--------------------------------------------
MST By Prim's Algorithm
A F B G C D E