-
[Python 자료구조 #고급정렬1] 셸 정렬(shell sort), 힙 정렬(heap sort)Programming 기초/Python 2023. 6. 1. 00:09
* 다양한 정렬 알고리즘
- 선택 정렬 : 입력의 크기에 따라 자료 이동 횟수가 결정된다.
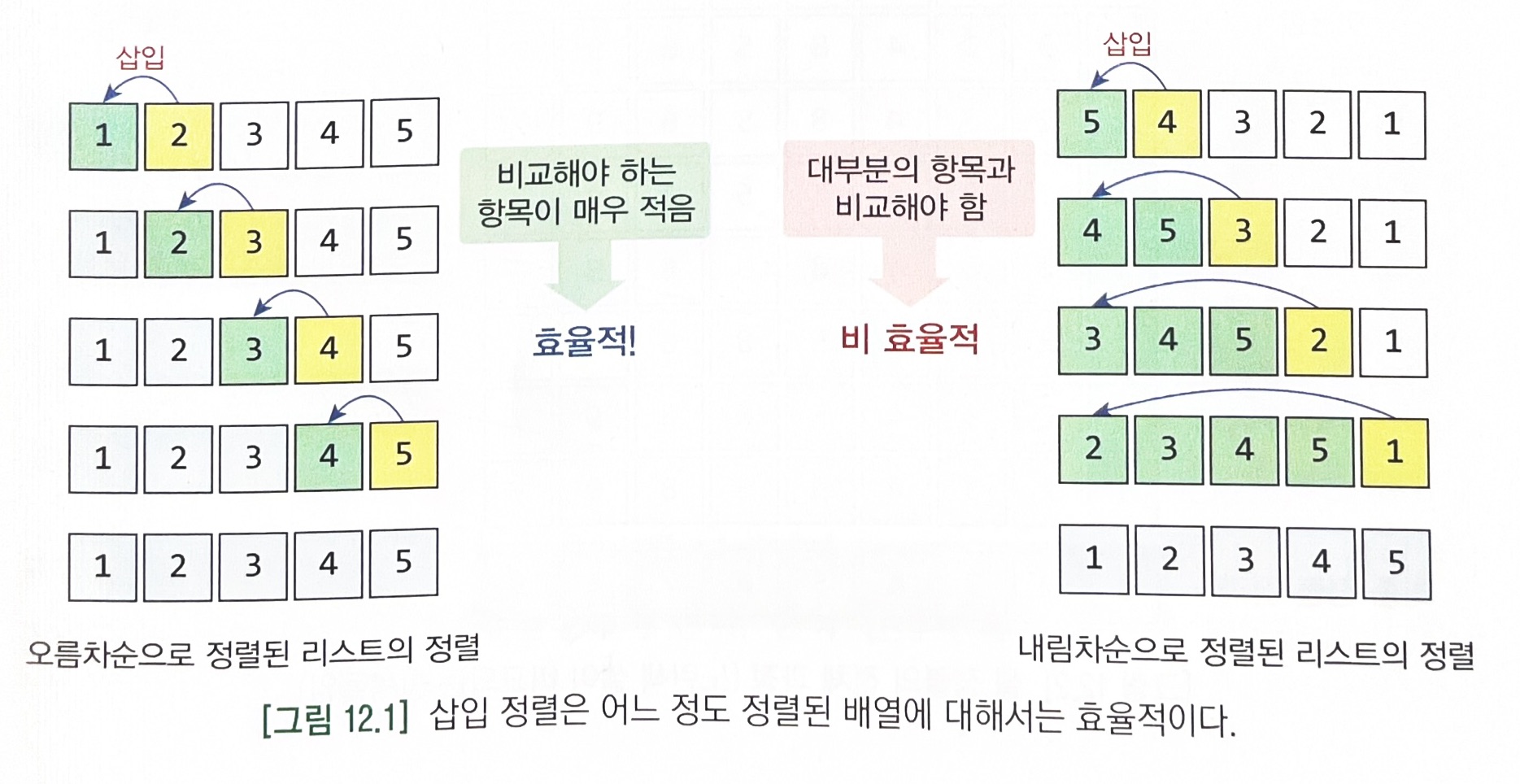
- 삽입 정렬 : 레코드의 많은 이동이 필요하지만 대부분의 레코드가 이미 정렬되어 있는 경우에는 비효율적이다.
- 버블 정렬 : 인접 요소를 교환하는 방식의 가장 간단한 알고리즘을 사용한다.
- 셸 정렬 : 삽입 정렬 개념을 개선한 방법
- 힙 정렬 : 추가적인 메모리 공간이 필요 없는 제자리 정렬로 구현하는 방법
- 병합 정렬 : 연속적인 분할과 병합을 이용하는 방법
- 퀵 정렬, 이중피벗 퀵 정렬 : 피벗을 이용한 정렬 방법으로 대표적인 효율적인 정렬 알고리즘
- 기수 정렬, 카운팅 정렬 : 항목의 비교를 사용하지 않고 분배를 이용해 정렬하는 방법이지만 적용할 수 있는 킷값에 제한이 있는 알고리즘
* 셸 정렬(shell sort)
- Donald L. Shell이 제안한 방법으로, 삽입정렬이 어느 정도 정렬된 배열에 대해서는 대단히 빠른 것에 착안했다.
- 셸 정렬은 배열 전체를 한꺼번에 정렬하지 않고 일종의 전처리를 한다.
- 셸 정렬은 먼저 리스트를 일정한 기준에 따라 여러 개의 부분 리스트로 나누고, 각 부분 리스트를 삽입 정렬을 이용해 정렬한다.
- 부분리스트는 전체 리스트에서 거리가 k만큼 떨어진 요소들로 이루어진다. 이 k를 간격(gap)이라고 하고, 부분 리스트의 개수와 같다.
- 실험적으로 시간 복잡도는 최악의 경우 O(n^2)이지만 평균적인 경우에는 O(n^1.5)이다.
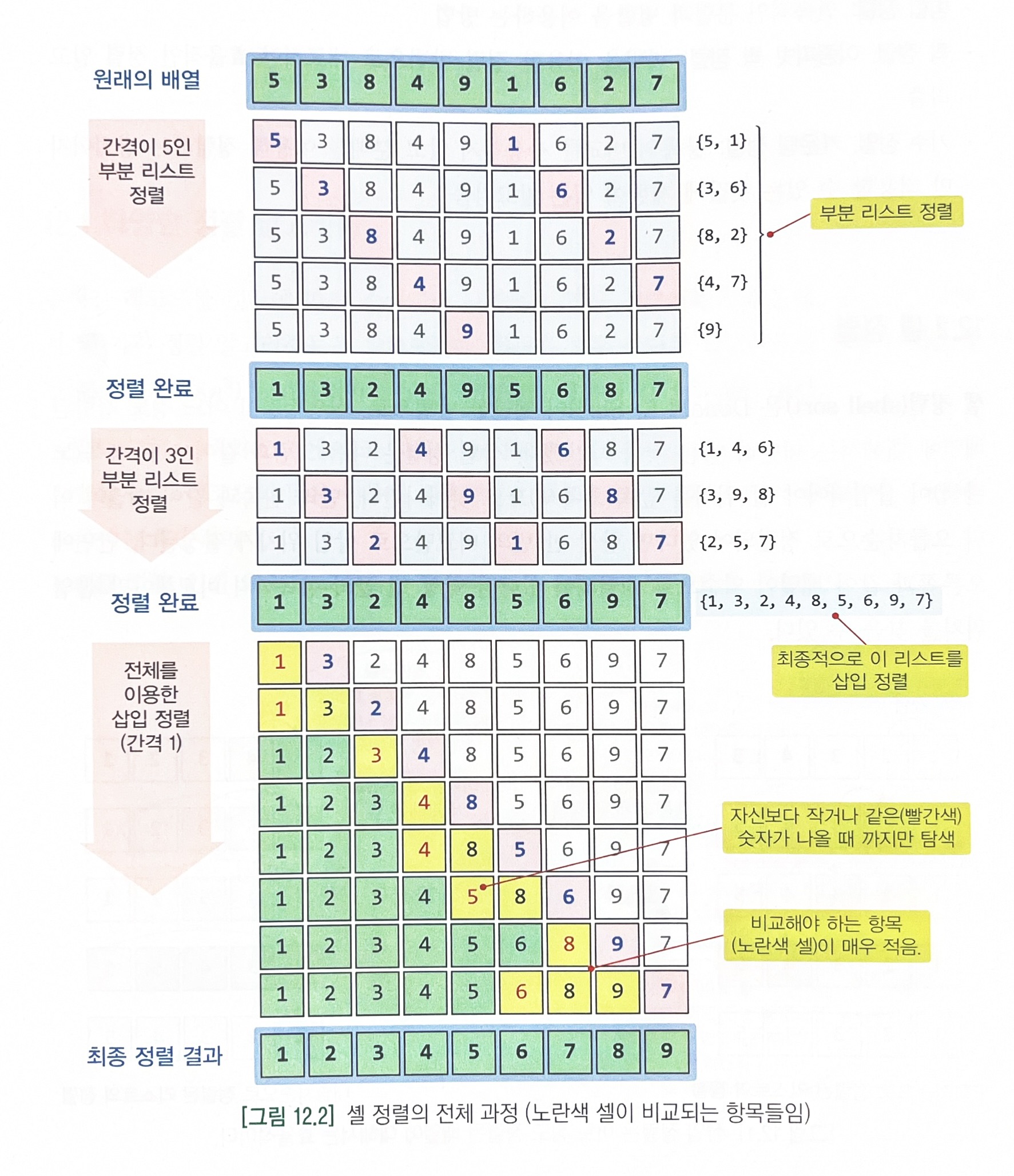
# 각 부분 리스트에 대하여 일정한 간격으로 떨어져 있는 요소들을 삽입 정렬을 이용해 정렬하는 함수 # gap 만큼 떨어진 요소들을 삽입 정렬. 정렬의 범위는 first에서 last def sortGapInsertion(A, first, last, gap): for i in range(first + gap, last + 1, gap): key = A[i] j = i - gap while j >= first and key < A[j]: # 삽입 위치를 찾음 A[j + gap] = A[j] # 항목 이동 j = j - gap A[j + gap] = key # 최종 위치에 삽입# 셸 정렬 알고리즘 def shell_sort(A): n = len(A) gap = n // 2 # 최초의 gap: 리스트 크기의 절반 while gap > 0: if (gap % 2) == 0: gap += 1 # gap이 짝수이면 1을 더함. # 간격이 짝수이면 +1을 하는 것이 좋다고 알려져있음. for i in range(gap): sortGapInsertion(A, i, n - 1, gap) print(" Gap=", gap, A) # 중간 결과 출력용 gap = gap // 2 # gap을 반으로 줄임(정수 나눗셈)data = [5, 3, 8, 4, 9, 1, 6, 2, 7] print("Original :", data) shell_sort(data) print("Shell :", data) ------------------------------------- Original : [5, 3, 8, 4, 9, 1, 6, 2, 7] Gap= 5 [1, 3, 2, 4, 9, 5, 6, 8, 7] Gap= 3 [1, 3, 2, 4, 8, 5, 6, 9, 7] Gap= 1 [1, 2, 3, 4, 5, 6, 7, 8, 9] Shell : [1, 2, 3, 4, 5, 6, 7, 8, 9]* 힙 정렬(heap sort)
- 힙은 우선순위 큐를 완전이진트리로 구현하는 방법으로 최댓값이나 최솟값을 쉽게 추출할 수 있는 자료구조이다.
- 정렬 과정은 단순히 정렬할 항목들을 모두 힙에 넣었다가 순서대로 꺼내는 것이다.
- n개의 항목을 삽입O(log_2 n) 하고 다시 삭제O(log_2 n)를 2n번 해야 하므로 정렬 시간 복잡도는 O(nlog_2 n)이다. ( 2n*log_2 n 이나, 시간 복잡도 개념에서 상수배는 무시한다.)
- 이 방법은 입력 데이터의 모든 항목을 다른 메모리 공간인 힙에 모두 넣었다가 빼야하므로, 입력 데이터의 크기에 비례하는 추가적인 메모리 공간이 필요하다.
MaxHeap 이전 포스팅 참고
import MaxHeap def heapSort1(data): # 최대 힙 사용 heap = MaxHeap.MaxHeap() # 모든 항목들을 힙에 넣음, 모듈이름.클래스 for n in data: heap.insert(n) # MaxHeap을 만들 때 편의상 인덱스 0번을 비우고 1번부터 스택을 쌓았다. for i in range(1, len(data) + 1): # 1, 2, ..., n data[-i] = heap.delete() # 맨 뒤에서 앞으로: -1, -2, ..., n* 제자리 정렬로 구현한 힙 정렬
- 추가적인 메모리를 사용하지 않는 제자리 정렬(in-place sorting)방식으로도 구현 할 수 있다.
- 입력 배열자체를 최대힙으로 먼저 만들고, 다음으로 오름차순으로 정렬시키는 방법이다.
- 전체 리스트 중에서 일부만 정렬할 필요가 있는 경우에 매우 유용하다.
- 시간 복잡도 O(nlog_2 n)
▶ 정렬되지 않은 배열 → 최대 힙
아래 그림에서 배열의 절반 이상은 트리에서 가족관계가 아니므로 서로 관련이 없다. 따라서 이미 힙을 이루고 있다고 생각할 수 있다.

heapify()는 현재 위치 i의 왼쪽 자식과 오른쪽 자식 중에서 더 큰 자식이 자신보다 크면 자신과 더 큰 자식을 교환하고, 순환호출을 이용하여 더 큰 자식에서 다시 이 과정을 반복한다.
# 다운힙을 위한 함수 heapify()를 순환을 이용해 구현. # 배열(arr), 배열의 길이(n), 다운힙을 진행하고자 하는 항목의 인덱스(i) def heapify(arr, n, i): largest = i # i번째가 가장 크다고 하자. l = 2 * i + 1 # 왼쪽 자식 인덱스: left = 2*i + 1(배열 0번을 사용함) r = 2 * i + 2 # 오른쪽 자식 인덱스: right = 2*i +2 (배열 0번을 사용함) if l < n and arr[i] < arr[l]: # 교환조건 검사 largest = l if r < n and arr[largest] < arr[r]: # 교환조건 검사 largest = r if largest != i: # 교환이 필요하면 arr[i], arr[largest] = arr[largest], arr[i] # 교환 heapify(arr, n, largest) # 순환적으로 자식노드로 내려감▶ 최대 힙 → 정렬되지 않은 배열
힙의 삭제는 루트를 삭제하는 것이다. 루트를 꺼내므로 항상 항목의 인덱스는 0으로 호출되어야 한다.
def heapSort(arr): n = len(arr) print("i=", 0, arr) # 중간결과 출력용 for i in range(n // 2, -1, -1): # 최대 힙을 만듦 : i: n//2, ..., 1, 0 heapify(arr, n, i) # heap 조건을 맞춤(downheap) print("i=", i, arr) # 중간결과 출력용 print() # 중간결과 출력용 for i in range(n - 1, 0, -1): arr[i], arr[0] = arr[0], arr[i] # 루트를 뒤쪽으로 옮김. 교체 heapify(arr, i, 0) # heap 조건을 맞춤(downheap) print("i=", i, arr) # 중간결과 출력용arr = [5, 3, 8, 4, 9, 1, 6, 2, 7] heapSort(arr) print("HeapSort: ", arr) ------------------------------------- # 최대 힙을 만드는 과정 i= 0 [5, 3, 8, 4, 9, 1, 6, 2, 7] i= 4 [5, 3, 8, 4, 9, 1, 6, 2, 7] i= 3 [5, 3, 8, 7, 9, 1, 6, 2, 4] i= 2 [5, 3, 8, 7, 9, 1, 6, 2, 4] i= 1 [5, 9, 8, 7, 3, 1, 6, 2, 4] i= 0 [9, 7, 8, 5, 3, 1, 6, 2, 4] # 최대 힙에서 맨 앞의 항목을 계속 꺼내 정렬하는 과정 i= 8 [8, 7, 6, 5, 3, 1, 4, 2, 9] i= 7 [7, 5, 6, 2, 3, 1, 4, 8, 9] i= 6 [6, 5, 4, 2, 3, 1, 7, 8, 9] i= 5 [5, 3, 4, 2, 1, 6, 7, 8, 9] i= 4 [4, 3, 1, 2, 5, 6, 7, 8, 9] i= 3 [3, 2, 1, 4, 5, 6, 7, 8, 9] i= 2 [2, 1, 3, 4, 5, 6, 7, 8, 9] i= 1 [1, 2, 3, 4, 5, 6, 7, 8, 9] HeapSort: [1, 2, 3, 4, 5, 6, 7, 8, 9]'Programming 기초 > Python' 카테고리의 다른 글