[Python 자료구조 #고급정렬2] 병합정렬(merge sort), 퀵 정렬(quick sort), 이중피벗 퀵 정렬(dual pivot quick sort)

* 병합 정렬(merge sort)

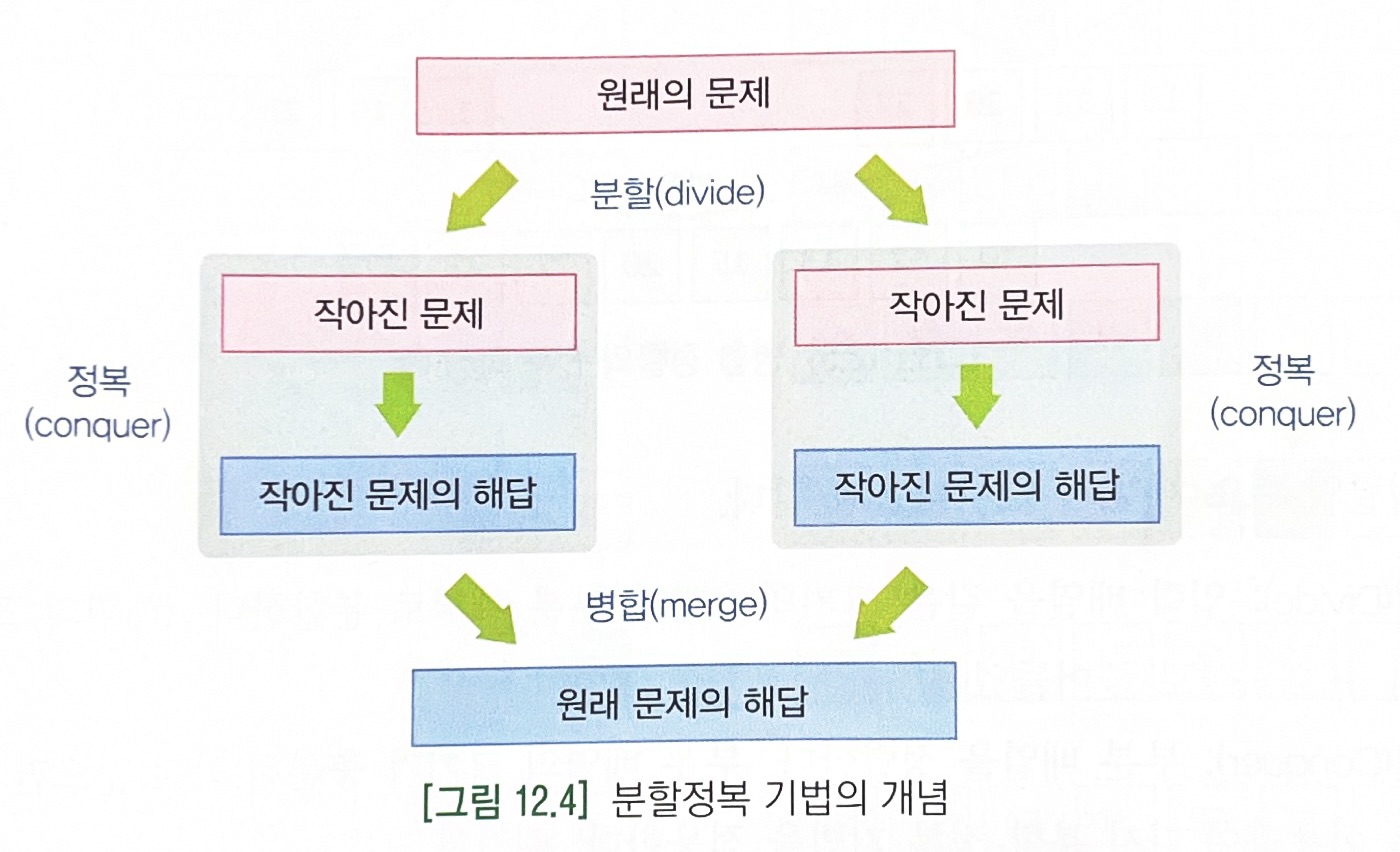
• 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 리스트를 합하여 전체가 정렬된 리스트를 만드는 방법이다.
• 하나의 문제를 작은 2개의 문제로 분리하고 각각 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략인 분할 정복(divide and conquer) 기법에 바탕을 두고 있다. 
• 추가적인 메모리가 필요하다는 단점이 있다.
• 병합단계에서 n번의 비교 연산이 필요하고, 병합 단계가 log_2 n번 필요하므로 비교 연산은 최대 O(n log_2 n)번 필요하다.
• 최악, 평균, 최선의 경우에도 모두 동일한 O(nlog_2 n)시간 복잡도를 갖는다.

▶ 병합 정렬의 주요 처리 과정

1. 분할(Divide) : 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
2. 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 기법을 적용한다. 배열의 크기가 1이면 이미 정복된 것이다.
3. 병합(Combine, merge): 정렬된 부분 배열들을 하나의 배열에 통합한다.

• 2개의 리스트를 병합(merge)하는 단계에서 실제로 정렬이 이루어진다.
• 병합을 위해서는 2개의 배열(A와 B)이 모두 반드시 정렬되어 있어야 한다.
• 두 배열의 요소들을 처음부터 하나씩 비교하여 두 요소 중에서 더 작은 요소를 새로운 배열 C로 옮기는 과정을 반복.( 새 배열이 필요하다)

# 병합 정렬 알고리즘을 이용해 배열을 오름차순으로 정렬하는 함수
def merge_sort(A, left, right):
    if left < right:
        mid = (left + right) // 2	# 리스트의 균등 분할
        merge_sort(A, left, mid)	# 부분 리스트 정렬
        merge_sort(A, mid + 1, right)	# 부분 리스트 정렬
        merge(A, left, mid, right)	# 병합

# 병합 함수
# A는 정렬하고자하는 리스트, left는 가장 왼쪽 인덱스, right는 가장 오른쪽 인덱스
def merge(A, left, mid, right):
    global sorted			# 병합을 위한 추가적인 배열
    k = left				# 배열 C(정렬된 리스트)의 인덱스
    i = left				# 배열 A의 인덱스
    j = mid + 1				# 배열 B의 인덱스
    while i <= mid and j <= right:
        if A[i] <= A[j]:
            sorted[k] = A[i]
            i, k = i + 1, k + 1
        else:
            sorted[k] = A[j]
            j, k = j + 1, k + 1

    if i > mid:						# 한쪽에 남아 있는 레코드의 일괄 복사
        sorted[k : k + right - j + 1] = A[j : right + 1]# 리스트의 슬라이싱 이용
    else:
        sorted[k : k + mid - i + 1] = A[i : mid + 1]	# 리스트의 슬라이싱 이용
    A[left : right + 1] = sorted[left : right + 1]	# sorted를 원래 배열 A에 복사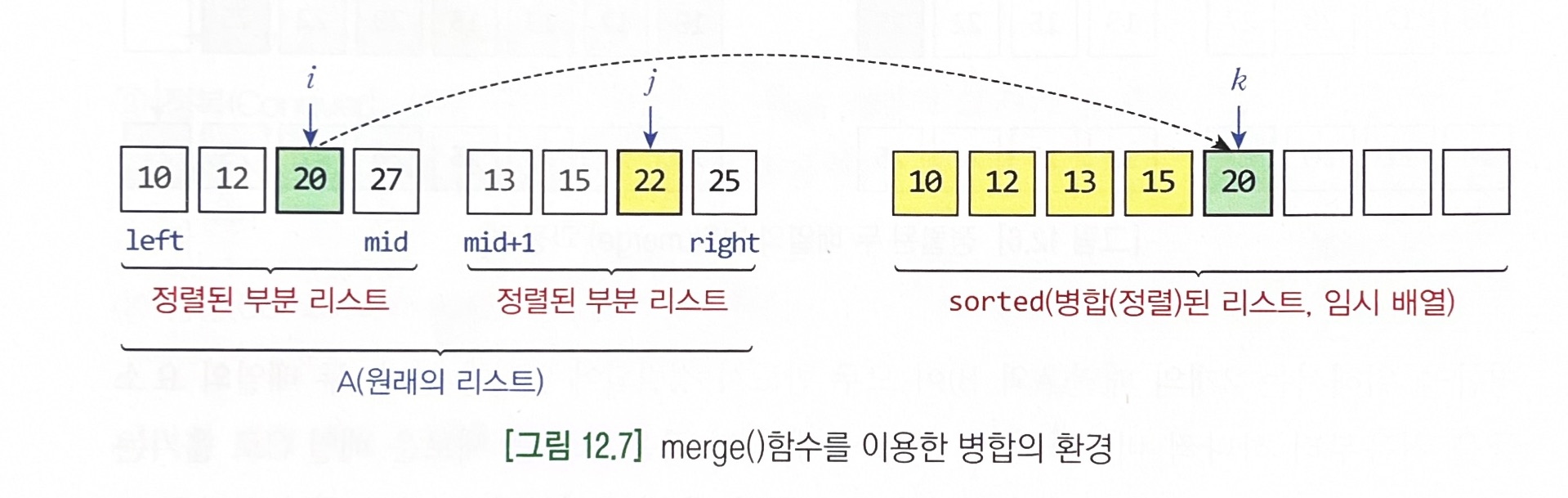

sorted = []
arr = [5, 3, 8, 4, 9, 1, 6, 2, 7]
sorted = [0] * len(arr)
merge_sort(arr, 0, len(arr) - 1)
print("MergeSort: ", arr)
---------------------------------------
MergeSort:  [1, 2, 3, 4, 5, 6, 7, 8, 9]

 

* 퀵 정렬(quick sort)

• 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법이다.
• 분할-정복법을 사용한다.
• 리스트 안에 있는 한 요소를 피벗(pivot)으로 선택하고, 피벗보다 작은 요소를 피벗의 왼쪽으로, 피벗보다 큰 요소를 피벗의 오른쪽으로 옮긴다. 이를 순환을 이용하여 리스트를 정렬한다. (여기서는 첫번째 요소를 피벗으로 선택한다.)
• 시간복잡도 최선의 경우 : 리스트 분할이 항상 리스트의 가운데에서 이루어지는 상황이다. O(n log_2 n)이다. 레코드의 이동 횟수는 비교 횟수보다 적으므로 무시할 수 있다. 
• 시간복잡도 최악의 경우 : 리스트가 계속 불균형하게 나누어지는 경우이다. (이미 정렬된 리스트의 경우) O(n^2)이다.
• 불균형 분할을 완화하기 위해서 리스트 내의 몇 개의 값들 중에서 중간값(median)을 피벗으로 선택하는 방법이 많이 사용된다.
• 퀵 정렬은 다른 O(n log_2 n)의 알고리즘과 비교해도 가장 빠른 것으로 알려져 있다.

 

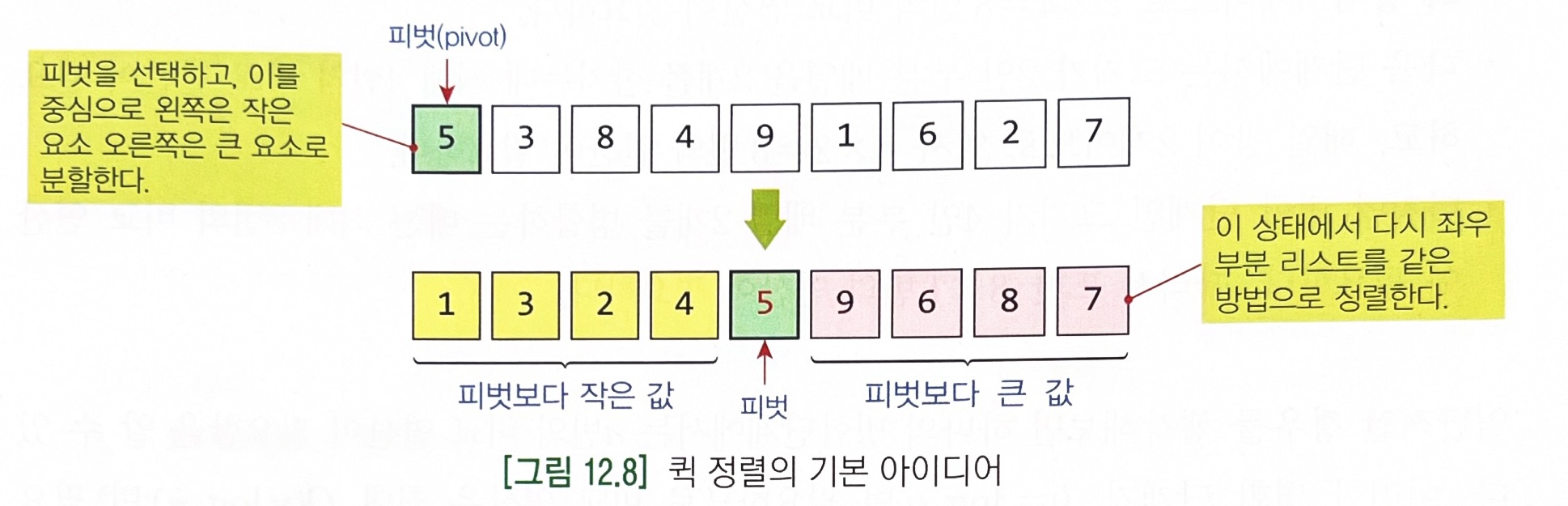
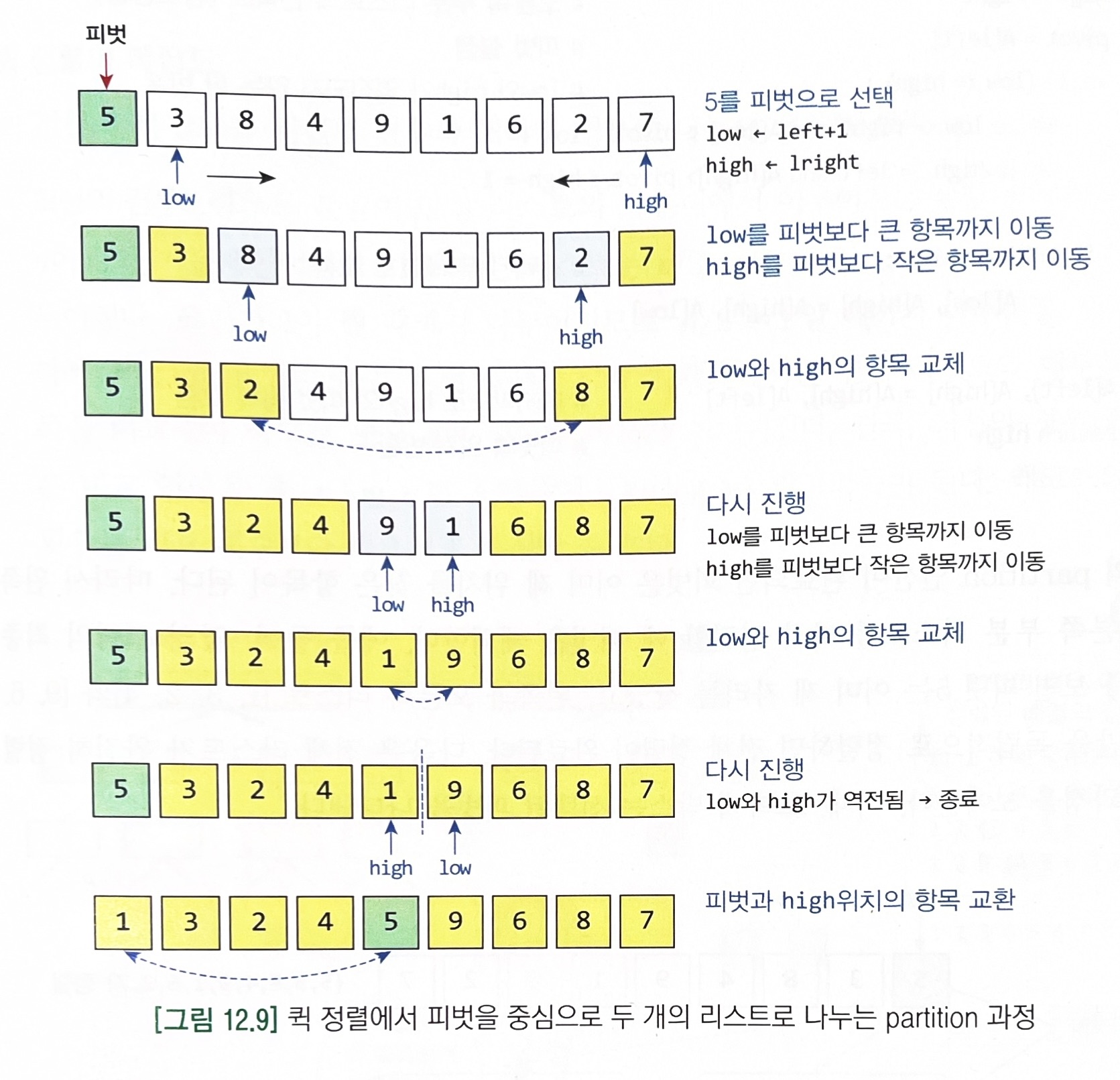
초록색 - 선택된 피벗

# 퀵 정렬 : 배열의 left ~ right 항목들을 오름차순으로 정렬하는 함수
def quick_sort(A, left, right):
    if left < right:				# 정렬 범위가 2개 이상인 경우
        q = partition(A, left, right)		# 좌우로 분할
        quick_sort(A, left, q - 1)		# 왼쪽 부분리스트를 퀵 정렬
        quick_sort(A, q + 1, right)		# 오른쪽 부분리스트를 퀵 정렬


# 퀵 정렬에서 피벗을 중심으로 두 개의 리스트로 나누는 partition 과정을 구현한 함수
def partition(A, left, right):
    low = left + 1				# 왼쪽 부분 리스트의 인덱스(증가방향)
    high = right				# 오른쪽 부분 리스트의 인덱스(감소방향)
    pivot = A[left]				# 피벗 설정
    while low <= high:				# low와 high가 역전되지 않는 한 반복
        while low <= right and A[low] <= pivot:
            low += 1
        while high >= left and A[high] > pivot:
            high -= 1

        if low < high:				# 선택된 두 레코드 교환
            A[low], A[high] = A[high], A[low]

    A[left], A[high] = A[high], A[left]		# 마지막으로 high와 피벗 항목 교환
    return high					# 피벗의 위치 반환

arr = [5, 3, 8, 4, 9, 1, 6, 2, 7]
quick_sort(arr, 0, len(arr) - 1)
print("quick_sort: ", arr)
-----------------------------------
quick_sort:  [1, 2, 3, 4, 5, 6, 7, 8, 9]

 

* 이중피벗 퀵 정렬(dual pivot quick sort)

• 퀵 정렬을 보완하여 2개의 피벗을 사용하는 퀵 정렬이다.
• 이론적인 시간 복잡도는 퀵 정렬과 차이가 없고, 최악의 경우의 시간 복잡도도 O(n^2)이다.
• 일반적인 경우 퀵 정렬보다 성능이 우수하다고 알려져 있어, 자바나 안드로이드의 시스템 정렬로 사용되었다.

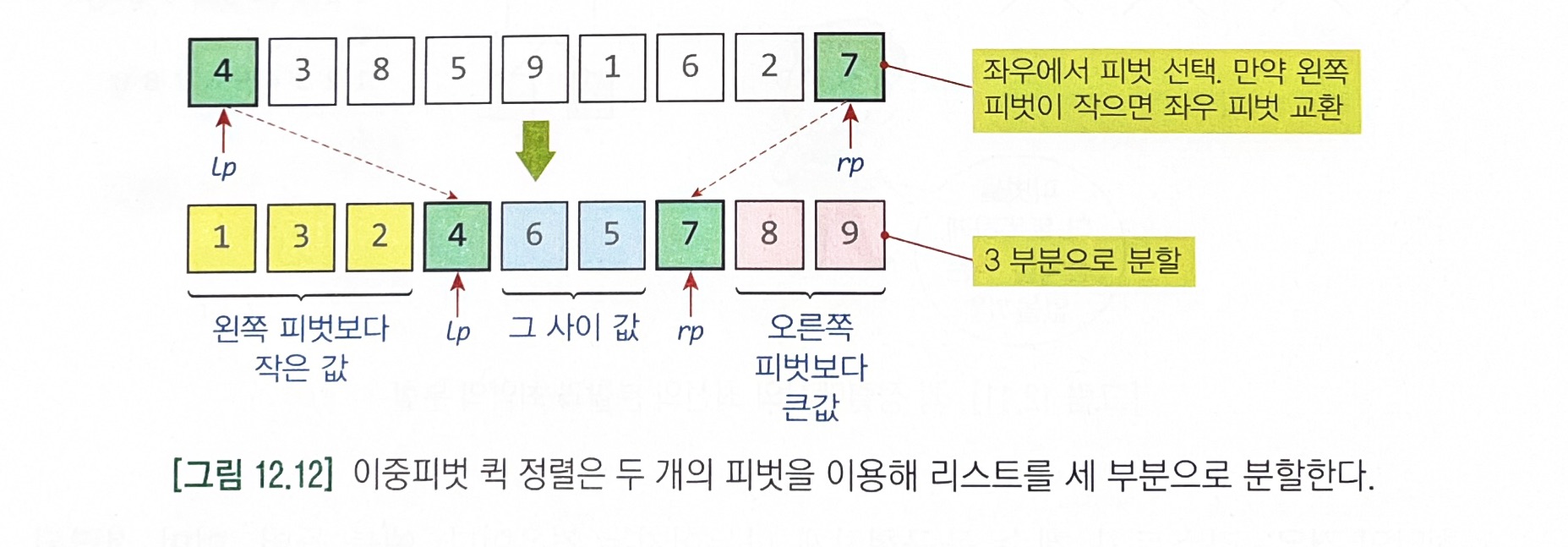
# 퀵 정렬
def dp_quick_sort(A, low, high):
    if low < high:			
        lp, rp = partitionDP(A, low, high)	# 좌우 피벗의 인덱스를 반환받음
        dp_quick_sort(A, low, lp - 1)
        dp_quick_sort(A, lp + 1, rp - 1)
        dp_quick_sort(A, rp + 1, high)

# 퀵 정렬에서 이중피벗을 중심으로 세 개의 리스트로 나누는 partition 과정을 구현한 함수
# A는 정렬하고자하는 리스트, low는 왼쪽 피벗의 인덱스, high는 오른쪽 피벗의 인덱스 
def partitionDP(A, low, high):
    if A[low] > A[high]:			# 오른쪽 피벗은 왼쪽보다 작지 않아야 함.
        A[low], A[high] = A[high], A[low]

    j = low + 1					# lp보다 작은 최대 인덱스
    g = high - 1				# rp보다 큰 최소 인덱스
    k = low + 1					# low+1부터 하나씩 증가
    lpVal = A[low]				# 왼쪽 피벗 값
    rpVal = A[high]				# 오른쪽 피벗 값
    while k <= g:			
        if A[k] < lpVal:			# A[k]가 왼쪽 피벗보다 작으면
            A[k], A[j] = A[j], A[k]		# 교환
            j += 1

        elif A[k] >= rpVal:			# 오른쪽 피벗보다 크거나 같으면
            while A[g] > rpVal and k < g:	# g의 위치를 찾은 후
                g -= 1
            A[k], A[g] = A[g], A[k]		#  A[k] <-> A[g]
            g -= 1

            if A[k] < lpVal:			# 변경된 A[k]가 왼쪽 피벗보다 작으면
                A[k], A[j] = A[j], A[k]		# 다시 교환
                j += 1
        k += 1

    j -= 1
    g += 1
    A[low], A[j] = A[j], A[low]			# 피벗을 제 위치로: j:왼쪽피벗
    A[high], A[g] = A[g], A[high]		# 피벗을 제 위치로: g:왼쪽피벗

    return j, g					# 왼쪽과 오른쪽 피벗의 인덱스 반환

arr = [7, 3, 8, 5, 9, 1, 6, 2, 4]
dp_quick_sort(arr, 0, len(arr) - 1)
print("dp_quick_sort: ", arr)
---------------------------------------
dp_quick_sort:  [1, 2, 3, 4, 5, 6, 7, 8, 9]