[Python 자료구조 #고급정렬3] 기수 정렬(radix sort), 카운팅 정렬(counting sort), 팀 정렬(Timsort)

* 기수 정렬(radix sort)

• 입력 데이터에 대해서 어떤 비교 연산도 실행하지 않고 데이터를 정렬할 수 있는 색다른 정렬 기법이다.
• 다른 방법들이 O(nlog_2 n)이라는 비교기반 정렬의 이론적인 하한선을 깰 수 없는데 비해 기수 정렬은 이 하한선을 깰 수 있다.
• 기수 정렬은 O(kn)의 시간 복잡도를 갖고 k에 비례한다. 대부분 k는 크지 않은 값(예: k<4)을 갖게 된다. (k는 자리수)
• 기수 정렬의 수행 시간은 정수의 크기와 관련이 있다. 32 비트 컴퓨터의 경우에는 십진법으로 대개 10개 정도의 자리수 많을 가지게 된다. 일반적으로 k는 n에 비하여 아주 작은 수가 되므로 기수 정렬은 O(n)이라고 하여도 무리가 없다.
• 추가적인 메모리를 필요로 한다.
• 기수(radix)란 숫자의 자리수이다. 예를 들면 숫자 42는 4와 2의 두 개의 자리수를 가지고, 이것이 기수가 된다.
• 낮은 자리수로 정렬한 다음 차츰 높은 자리수로 정렬해야 한다.

아래 코드에서는 0인덱스를 포함한다.

• 십진법에서 버킷은 10개, 2진법에서는 버킷 2개. 단 2진법에서는 패스 수가 훨씬 많아질 것이다.
• 리스트 상에 있는 요소들의 상대적인 순서가 유지되어야 하기 때문에 버킷은 큐로 구현된다.

* 큐를 사용하는 방법 3가지(여기선 2번째 방법 사용)
1. 이전 포스팅에서 직접 구현한 원형큐 클래스 CircularQueue
2. 파이썬 queue 모듈의 Queue 클래스
3. collections 모듈의 deque 클래스를 큐처럼 사용하는 방법.

from queue import Queue		# 파이썬 queue 모듈의 Queue 사용

# 기수 정렬
# BUCKETS과 DIGITS는 외부에서 따로 지정.
def radix_sort(A):					# 큐의 리스트
    queues = []
    for i in range(BUCKETS):				
        queues.append(Queue())				# BUCKETS개의 큐 사용

    n = len(A)
    factor = 1						# 1의 자리부터 시작
    for d in range(DIGITS):				# 모든 자리에 대해 (외부 루프 반복 횟수=DIGITS)
        for i in range(n):				# 자릿수에 따라 큐에 삽입
            queues[(A[i] // factor) % 10].put(A[i])	# 숫자를 삽입
        i = 0
        for b in range(BUCKETS):			# 버킷에서 꺼내어 원래의 리스트로
            while not queues[b].empty():		# b번째 큐가 비어있지 않는 동안.
                A[i] = queues[b].get()			# 원소를 꺼내 리스트에 저장
                i += 1
        factor *= 10					# 그 다음 자리수로 간다.
        print("step", d + 1, A)				# 중간 과정 출력용 문장

1에서 9999 사이의 숫자 10개를 무작위로 생성하고 기수 정렬로 정렬하는 테스트 코드

10진법을 사용하고 최대 네 자리 10진수 숫자이므로 BUCKETS는 10이 되어야 하고, DIGITS는 4 이상이면 된다.

난수 발생 함수 randint()를 사용하기 위해 random 모듈을 포함하였다.

import random

BUCKETS = 10
DIGITS = 4
data = []
for i in range(10):
    data.append(random.randint(1, 9999))	# 1~ 9999 사이의 숫자 10개 생성
radix_sort(data)				# 기수 정렬
print("Radix: ", data)				# 결과 출력
--------------------------------------------------------------------
# 일, 십, 백, 천의 자리 순으로 정렬
step 1 [1150, 3612, 4942, 5324, 2004, 325, 205, 9217, 38, 3439]     
step 2 [2004, 205, 3612, 9217, 5324, 325, 38, 3439, 4942, 1150]     
step 3 [2004, 38, 1150, 205, 9217, 5324, 325, 3439, 3612, 4942]     
step 4 [38, 205, 325, 1150, 2004, 3439, 3612, 4942, 5324, 9217]     
# 최종 정렬 결과
Radix:  [38, 205, 325, 1150, 2004, 3439, 3612, 4942, 5324, 9217]

 

* 카운팅 정렬(counting sort)

• 정렬을 위한 키 값들이 일정한 범위를 가진 정수라면 카운팅 정렬을 사용해 정렬할 수 있다.
• 카운팅 정렬은 기본적으로 키 값을 가진 항목의 수를 세는 방법을 이용한다. (키 값의 비교를 사용하지 않는다.)
• 카운팅 정렬은 입력 데이터가 크지 않은 일정한 범위의 값을 가진 양수라면 매우 효율적이다.
• 입력 리스트가 n개의 정수를 가지고 있고, 숫자의 범위가 k가지(0~k-1)라면 전체 알고리즘은 O(k+n)의 시간 복잡도를 갖는다. k가 작은 수로 제한된다면 시간 복잡도는 O(n)이라고 할 수 있다.
• 입력 배열에 추가적으로 (k+n)의 메모리 공간을 필요로 한다. 만약 k가 매우 크다면 매우 많은 공간이 추가로 필요로 하게 된다. (k의 크기와 공간복잡도가 비례한다.)
• 키 값이 음수인 경우도 가능하다. 가장 작은 음수를 0으로 만드는 값을 모든 키 값에 더해 모든 항목을 양수로 만든 후 카운팅 정렬을 적용하면 된다.

 

▶ 카운팅 정렬 예시

0. 키 값이 0 ~ 9까지라고 가정하고, 입력 배열 [1, 4, 1, 2, 7, 5, 2]라고 하자.

1. 입력 배열 키 값 항목들을 세서, Count 배열을 채운다. 

인덱스	0	1	2	3	4	5	6	7	8	9
COUNT	0	2	2	0	1	1	0	1	0	0

 2. count 배열을 0에서부터 차례대로 누적값으로 갱신한다. 

인덱스	0	1	2	3	4	5	6	7	8	9
COUNT	0	2	4	4	5	6	6	7	7	7

3. 최종(출력) 배열을 만든다. 0은 없고, 1은 인덱스 2 이전까지 (0,1)을 채운다. 2는 그 다음부터 인덱스 4이전까지 (2,3)을 채운다. 3은 4이전까지 채워야 하는데, 인덱스 3까지 이미 채워져 있으니까 입력 배열에 없다는 것이다.

인덱스	0	1	2	3	4	5	6
COUNT	1	1	2	2	4	5	7

 

 

MAX_VAL = 1000					# 키 값< MAX_VAL

# 카운팅 정렬
def counting_sort(A):
    output = [0] * MAX_VAL			# 정렬 결과를 저장
    count = [0] * MAX_VAL			# 각 숫자의 빈도를 저장

    for i in A:					# 각 숫자별 빈도를 계산
        count[i] += 1

    for i in range(MAX_VAL):			# count[i]가 출력 배열에서
        if i != 0:	# i=0일때 count[i-1]은 MAX_VAL-1값을 가리키게 되므로 이를 방지하기 위함.
       	    count[i] += count[i - 1]		# 해당 숫자의 위치가 되도록 수정

    for i in range(len(A)):			# 정렬된 배열 만들기
        output[count[A[i]] - 1] = A[i]
        count[A[i]] -= 1

    for i in range(len(A)):			# 정렬 결과를 원래 배열에 복사
        A[i] = output[i]

 

 

 

 

* 팀 정렬(Timsort)

1993년 Peter Mcllroy의 논문에서 제시된 기법들을 2002년에 팀 피터스(Tim Peters)가 파이썬 언어에서 사용하기 위해 구현한 정렬 방법이다.

• 삽입 정렬과 병합 정렬에 기반을 둔 하이브리드 알고리즘. 
• 하이브리드 정렬(hybrid sort) : 두 가지 이상의 알고리즘을 섞은 정렬 알고리즘
• 파이썬의 기본 정렬 알고리즘인 sorted()함수와 sort() 메소드로 사용되고 있다.
• O(n) ~ O(nlog_2 n)의 시간 복잡도를 보장한다.

▶ 팀 정렬 알고리즘
팀 정렬에서는 런(run)이란 개념을 사용한다. 정렬 과정 진행 전에 입력데이터를 스캔하면서 오름차순(non-decreasing order)이나 내림차순(strictly decreasing order)으로 구성된 데이터 묶음을 찾고, 이들을 스택에 저장한다.(이때, 내림차순의 데이터는 순서를 뒤집는다.) 런들이 준비가 되면 스택의 런들에 대해 조건에 따른 병합을 진행한다. 이때, 런의 크기가 최소 크기(minimum run size)보다 작으면 삽입정렬을 사용하고, 그렇지 않으면 병합 정렬을 사용한다. 이러한 병합 과정은 최종적으로 스택의 런이 하나가 될 때까지 반복된다.

▶ 병합과정에서의 최적화 기법 
두 개의 런 A와 B를 병합할 때, A의 어떤 원소에 해당하는 위치를 B에서 찾기 위해 이진 탐색을 적용한다. 
또, 한쪽 런의 항목이 일정 횟수 이상으로 연속적으로 선택되어 병합되면 갤로핑(galloping)모드를 활성화하여 데이터를 묶음으로 한꺼번에 옮길 수 있는 방법도 사용한다.

 

*정렬 알고리즘들의 성능 분석

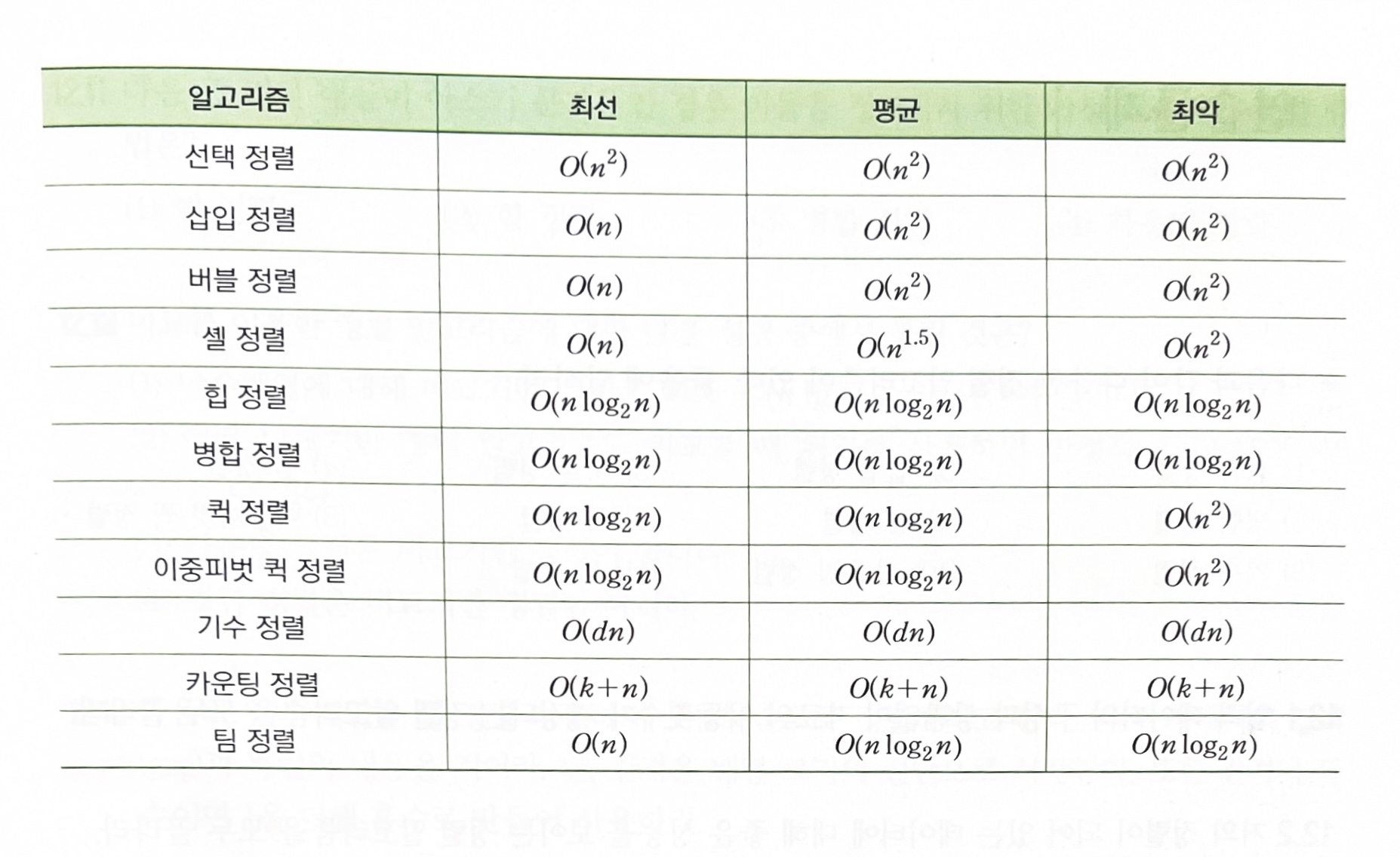
출처 : 파이썬으로 쉽게 풀어쓴 자료구조