[Python 자료구조 #가중치 그래프1] 인접행렬/인접리스트를 이용한 가중치 그래프 표현

* 가중치 그래프(weighted graph)

• 간선에 비용이나 가중치가 할당된 그래프.
• 수학적으로 G = (V, E, w)와 같이 표현된다. 
• V(G)는 그래프 G의 정점들의 집합
• E(G)는 그래프 G의 간선들의 집합
• w(e)는 간선 e의 강도(weight)로 비용(cost) 또는 길이(length)라고도 부른다.
• 어떤 가중치 그래프의 경로를 p = (v_0, v_1, ..., V_k)라고 한다면, 경로의 길이(또는 강도) w(p)는 다음과 같이 경로상의 모든 간선의 길이 합으로 표현된다.

* 인접 행렬을 이용한 가중치 그래프 표현

▶ 간선이 없느 것을 표기하는 방법

1. 무한대(INF)

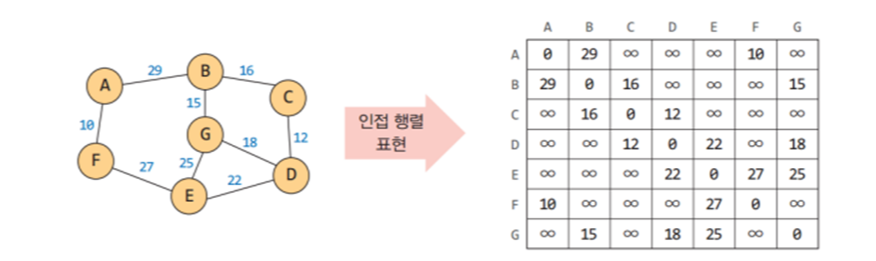
2. None

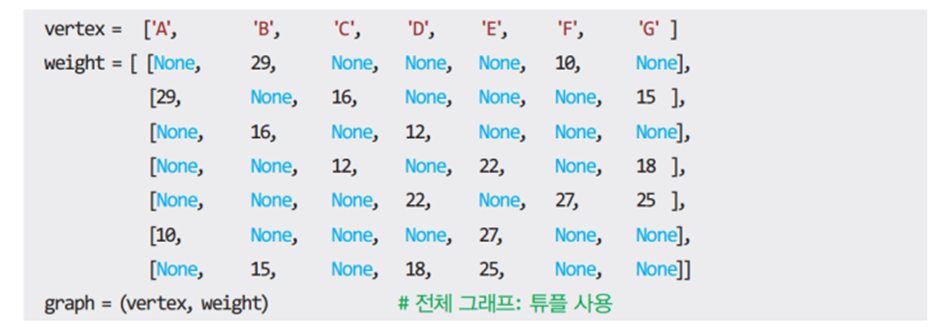
▶ 인접 행렬에서의 가중치의 합 계산

# 인접 행렬에서의 가중치의 합 계산
# 
def weightSum( vlist, W ):			# 매개변수 : 정점 리스트, 인접 행렬
    sum = 0					# 가중치의 합
    for i in range(len(vlist)) :		# 모든 정점에 대해(i: 0, ... N-1)
        for j in range(i+1, len(vlist)):	# 하나의 행에 대해(삼각영역만. 0부터가 아닌 i+1부터!!)
            if W[i][j] != None :		# 만약 간선이 있으면
                sum += W[i][j]			# sum에 추가
    return sum					# 전체 가중치 합을 반환

vertex =   ['A',    	'B',    'C',    'D',    'E',    'F',    'G' ]
weight = [ [None,	29,	None,	None,	None,   10,		None],
           [29,		None,	16,		None,	None,	None,	15  ],
           [None,	16,		None,	12,		None,	None,	None],
           [None,	None,   12,		None,	22,		None,	18  ],
           [None,	None,	None,   22,		None,	27,		25  ],
           [10,		None,	None,	None,   27,		None,	None],
           [None,  	15,		None,   18,		25,		None,	None]]    
graph = (vertex, weight)		# 전체 그래프 : 튜플 사용

print('AM : weight sum = ', weightSum(vertex, weight))
---------------------------------------------------------------------
AM : weight sum =  174

 

▶ 인접 행렬에서의 모든 간선 출력

def printAllEdges(vlist, W ):			  	# 매개변수 : 정점 리스트, 인접 행렬
    for i in range(len(vlist)) :
        for j in range(i+1, len(W[i])) :		# 모든 간선 W[i][j]에 대해(중복 없이 삼각영역만!!)
            if W[i][j] != None and W[i][j] != 0 :	# 간선이 있으면
                print("(%s,%s,%d)"%(vlist[i],vlist[j],W[i][j]), end=' ')
                # 간선은 양쪽 정점 이름과 가중치를 함께 출력한다.
    print()

printAllEdges(vertex, weight)
-------------------------------------------------------------------------
(A,B,29) (A,F,10) (B,C,16) (B,G,15) (C,D,12) (D,E,22) (D,G,18) (E,F,27) (E,G,25)

 

* 인접 리스트를 이용한 가중치 그래프 표현

• 정점과 가중치는 (정점, 가중치)의 형태로 튜플로 표현하는 것이 좋다.
• 딕셔너리 엔트리의 키(key)는 정점 데이터, 값(value)은 간선의 집합이 된다.
• 간선의 집합은 (인접 정점, 가중치)의 튜플을 원소로 갖는다.

인접 리스트를 이용한 가중치 그래프의 표현 예

 

▶ 인접 리스트에서의 가중치의 합 계산

def weightSum(graph):		# 가중치의 총 합을 구하는 함수
    sum = 0
    for v in graph:             # 그래프의 모든 정점 v에 대해 : 'A', 'B', ...
        for e in graph[v]:      # v의 모든 간선 e에 대해: ('B', 29), (정점, 가중치)
            sum += e[1]		# sum에 추가
    return sum//2		# 하나의 간선이 두 번 더해지므로 2로 나눔

graphAL ={'A' : set([('B',29),('F',10)          ]),
        'B' : set([('A',29),('C',16), ('G',15)]),
        'C' : set([('B',16),('D',12)          ]),
        'D' : set([('C',12),('E',22), ('G',18)]),
        'E' : set([('D',22),('F',27), ('G',25)]),
        'F' : set([('A',10),('E',27)          ]),
        'G' : set([('B',15),('D',18), ('E',25)]) }

print('AL : weight sum = ', weightSum(graphAL))
----------------------------------------------------
AL : weight sum =  174

 

▶ 인접 리스트에서의 간선 출력

def printAllEdges(graph):		# 모든 간선을 출력하는 함수
    for v in graph:             # 그래프의 모든 정점 v에 대해 : 'A', 'B', ...
        for e in graph[v]:      # v의 모든 간선 e에 대해: ('B', 29), ...
            print("(%s,%s,%d)"%(v,e[0],e[1]), end=' ')

printAllEdges(graphAL)
--------------------------------------------------------
(A,F,10) (A,B,29) (B,A,29) (B,C,16) (B,G,15) (C,B,16) (C,D,12) 
(D,G,18) (D,C,12) (D,E,22) (E,G,25) (E,F,27) (E,D,22) (F,E,27) 
(F,A,10) (G,E,25) (G,B,15) (G,D,18)