[cs231n_review#Lecture 2-5] Linear Classifier from viewpoint of the template matching approach

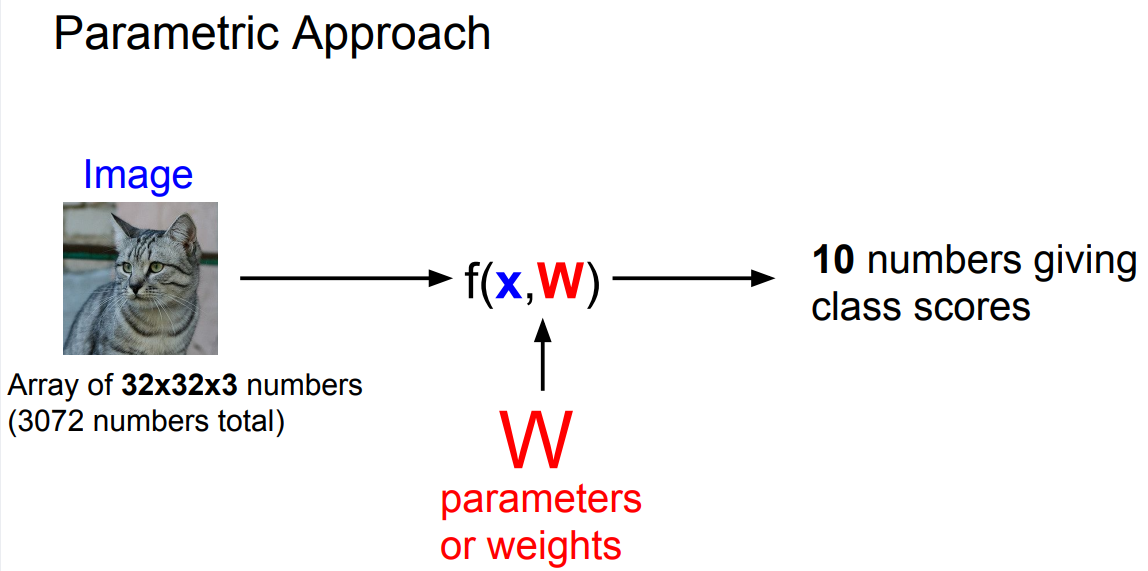
In linear classification, we're going to take a bit of a different approach from k-nearest neighbor. So, the linear classifier is one of the simplest examples of what we call a parametric model.

 

we usually write as X for our input data, and also a set of parameters, or weights, which is usually called W, also sometimes theta, depending on the literature.

 

So, in the k-nearest neighbor setup there was no parameters, instead, we just kind of keep around the whole training data, the whole training set, and use that at test time. But now, in a parametric approach(Linear classification), we're going to summarize our knowledge of the training data and stick all that knowledge into these parameters, W.

 

And now, at test time, we no longer need the actual training data, we can throw it away. We only need these parameters, W, at test time. So this allows our models to now be more efficient and actually run on maybe small devices like phones.

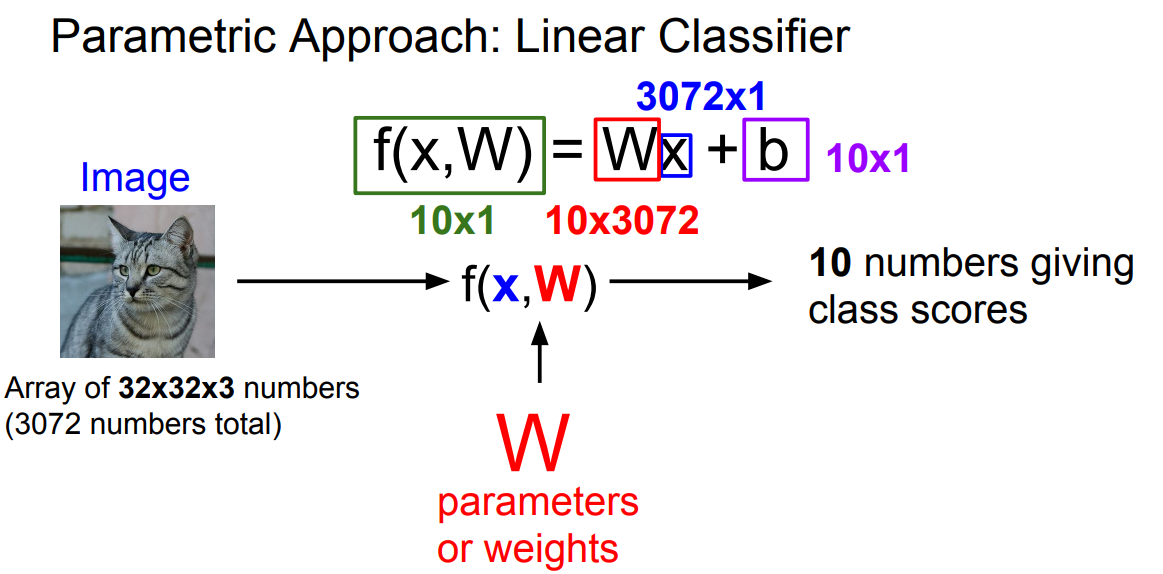
the simplest possible example of combining these two things is just, maybe, to multiply them. And this is a linear classifier. So here our F of X, W is just equal to the W times X.

 

if you kind of unpack the dimensions of these things, we recall that our image was maybe 32 by 32 by 3 values. so then, we're going to take those values and then stretch them out into a long column vector that has 3,072 by one entries. and now we want to end up with 10 class scores. We want to end up with 10 numbers for this image

 

We want to end up with 10 numbers for this image giving us the scores for each of the 10 categories. Which means that now our matrix, W, needs to be ten by 3072.

 

* a bias term

we'll often add a bias term which will be a constant vector of 10 elements that does not interact with the training data, and instead just gives us some sort of data independent preferences for some classes over another.

 

* a bias term example

So you might imagine that if you're dataset was unbalanced and had many more cats than dogs, for example, then the bias elements corresponding to cat would be higher than the other ones. 

 

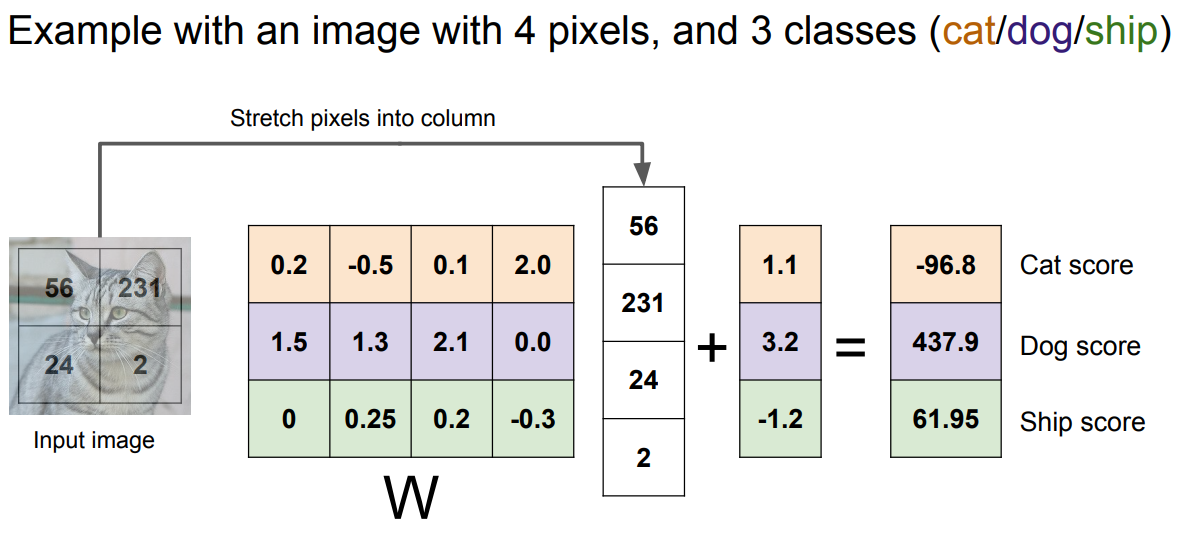
and now, in this example, we are just restricting to three classes, cat, dog, and ship, because you can't fit 10 on a slide, and now our weight matrix is going to be four by three, so we have four pixels and three classes. And now, again, we have a three element bias vector that gives us data independent bias terms for each category.

 

So, when you look at it this way you can kind of understand linear classification as almost a template matching approach. Where each of the rows in this matrix correspond to some template of the image. And now the enter product or dot product between the row of the matrix and the column giving the pixels of the image, computing this dot product kind of gives us a similarity between this template for the class and the pixels of our image. and then bias just, again, gives you this data independence scaling offset to each of the classes.

 

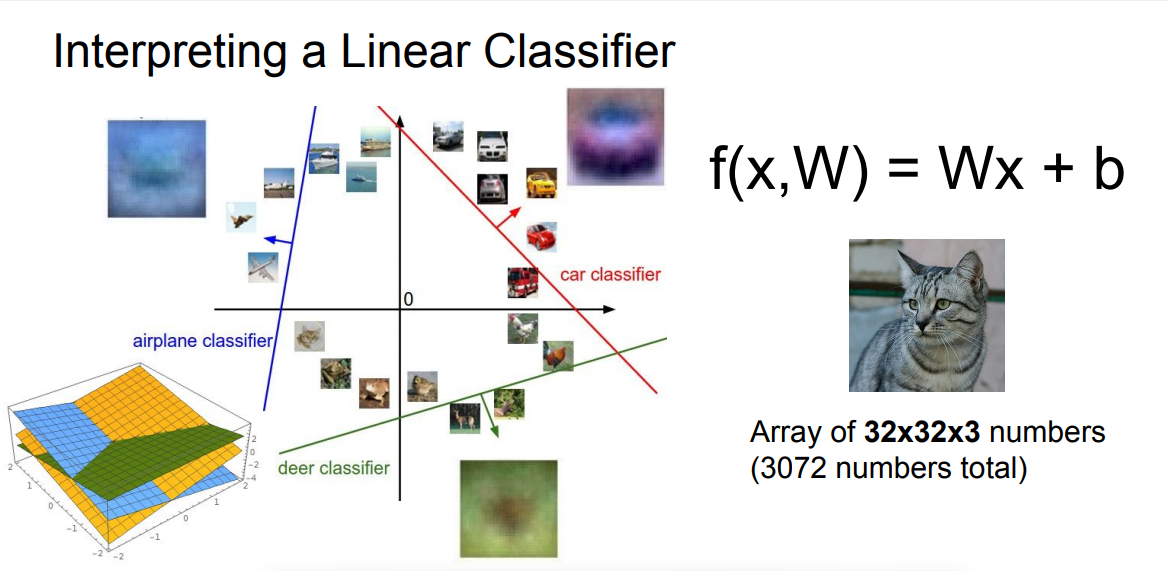
If we think about linear classification from this viewpoint of template matching we can actually take the rows of that weight matrix and unravel them back into images and actually visualize those templates as images. And this gives us some sense of what a linear classifier might actually be doing to try to understand our data.

 

* linear classificaion example from viewpoint of template matching 

So, for example, on the bottom left, we see the template for the plane class, kind of consists of this like blue blob, this kind of blobby thing in the middle and maybe blue in the background, which gives you the sense that this linear classifier for plane is maybe looking for blue stuff and blobby stuff, and those features are going to cause the classifier to like planes more.

 

Or if we look at this car example, we kind of see that there's a red blobby thing through the middle and a blue blobby thing at the top that maybe is kind of a blurry windshield. But this is a little bit weird, this doesn't really look like a car. No individual car actually looks like this.

 

* problem 1 of linear classifier 

So the problem is that the linear classifier is only learning one template for each class. So if there's sort of variations in how that class might appear, it's trying to average out all those different variations, all those different appearances, and use just one single template to recognize each of those categories.

 

We can also see this pretty explicitly in the horse classifier. So in the horse classifier we see green stuff on the bottom because horses are usually on grass. And then, if you look carefully, the horse actually seems to have maybe two heads, one head on each side. And I've never seen a horse with two heads. But the linear classifier is just doing the best that it can, because it's only allowed to learn one template per category.

 

And as we move forward into neural networks and more complex models, we'll be able to achieve much better accuracy because they no longer have this restriction of just learning a single template per category.

 

 

Another viewpoint of the linear classifier is to go back to this idea of images as points and high dimensional space. And you can imagine that each of our images is something like a point in this high dimensional space. And now the linear classifier is putting in these linear decision boundaries to try to draw linear separation between one category and the rest of the categories.

 

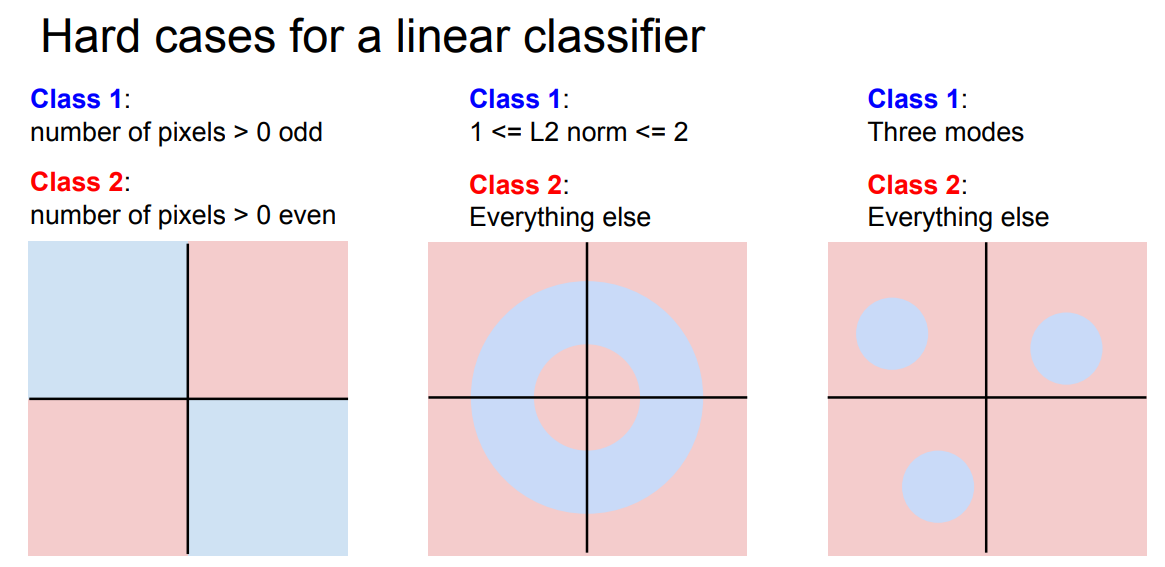
* problem 2 of linear classifier 

One example, on the left here, is that, suppose we have a dataset of two categories, and these are all maybe somewhat artificial, blue and red. if you actually go and draw what these different decisions regions look like in the plane, you can see that our blue class with an odd number of pixels is going to be these two quadrants in the plane, and even will be the opposite two quadrants.

 

So now, there's no way that we can draw a single linear line to separate the blue from the red. So this would be an example where a linear classifier would really struggle. So this kind of a parity problem of separating odds from evens is something that linear classification really struggles with traditionally.

 

Other situations where a linear classifier really struggles are multimodal situations. So here on the right, maybe our blue category has these three different islands of where the blue category lives, and then everything else is some other category. Where there's maybe one island in the pixel space of horses looking to the left, and another island of horses looking to the right. and now there's no good way to draw a single linear boundary between these two isolated islands of data. So anytime where you have multimodal data, like one class that can appear in different regions of space, is another place where linear classifiers might struggle.