[DL for VS #3] 최적화 알고리즘-(배치, 확률적, 미니배치)경사하강법, 역전파 알고리즘

2.6.2 배치 경사 하강법(batch gradient descent, BGD)

1.경사 (경사=미분=기울기 )

가장 가파른 방향을 찾는다. 3차원으로 생각해보면 여러 편미분값 중 가장 가파른(가장 큰 편미분값) 방향을 선정하는 것.

 

2.보폭(학습률 α)

학습률(learning rate)은 경사하강법 수행 중 가중치를 수정할 때 이동할 보폭에 해당. 가장 중요한 하이퍼파라미터 중 하나.

학습률 크면 신경망 학습 빠르게 진행(오차 함수의 언덕을 큰 보폭으로 내려가므로)

학습률이 너무 크면 보폭 사이에 골이 존재할 경우 오찻값이 진동(oscillating)하기만 할 뿐 감소하지 않는다.

학습률이 너무 작으면 학습 시간이 오래 걸림.

학습률은 0.1 또는 0.01을 초깃값으로 설정한 다음 추후 조정.

 

3.방향(경사)과 보폭(학습률) 합치기

방향과 보폭을 곱하면 각 단계의 가중치 변화량을 계산할 수 있음.

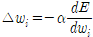
기호가 마이너스인 이유는 경사는 항상 올라가는 방향이기 때문. 우리는 경사를 내려가야 하므로 경사의 반대 방향으로 이동해야 한다. 

4.배치 경사 하강법의 문제점

1)지역 극소점(local minima)이 여러개면 전역 최소점(global minima) 찾기 힘듦.

2)경사를 계산하기 위해 매번 훈련 데이터 전체를 사용한다는 점.

    *두 가지 문제를 해결하기 위해 고안된 것이 확률적 경사 하강법이다.

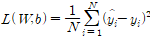
위와같이 정의되는 손실함수에서 훈련샘플 수가 1억 개면 가중치를 한 번 수정하기 위해 1억 개의 손실값을 합해야 한다. 훈련 데이터 전체를 하나의 배치로 사용하기 때문에 배치 경사 하강법이라고 부름.

 

예를들어 위 주택 가격 예측 신경망을 가져와서 25개의 가중치가 있다고 하자. 훈련샘플(주택 정보)은 10개(a,b,c,,,)를 가지고 있다고 하자.

 

< 배치 경사하강법 프로세스 >

(1) 초기 가중치는 임의의 값을 부여.

(2) 하나의 가중치행렬을 임의로 선정.((w1,w2,w3,,,w25) 즉, 1X25 행렬을 의미(행은 요소를, 열은 차원을 의미))

(3) 그 오차함수에 대한 가중치행렬의 미분을 계산함.

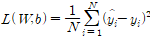
(N은 샘플 개수가 아닌 출력 층의 노드 수를 의미)

모든 훈련샘플에 대한 병렬 연산 (=1배치 연산) 후

전체 오차를 계산한다.

즉 가중치를 한 번 수정하기 위해(1배치) 모든 샘플에 대한 오차의 합(전체오차) 계산해야한다.

(4) 학습률만큼 이동하여 수정된 가중치행렬에 대해 다시 손실함수의 미분을 계산을 n번의 에포크 동안 반복.(1-3를 n번 반복) -> 총 n번의 가중치 업데이트가 일어남.

(주의)
여기까지는 역전파를 적용하지 않고 온전한 순전파임.(다층이므로 무조건 역전파를 적용해야하나 설명의 편의를 위해 단층 퍼셉트론의 개념으로 경사하강법을 설명했음. 실제론 다층이므로 각 가중치가 서로 독립(다음 층의 가중치들은 이전 층의 가중치에 종속되어있다.)이 아니므로 단층 퍼셉트론에서처럼 단순히 ∆w를 더하는 방식으로 가중치를 업데이트 하면 안 됨. 그래서 다층 퍼셉트론(MLP)에서는 체인 룰을 이용하여 가중치를 구해야 한다.

 

2.6.3 확률적 경사 하강법(Stochastic Gradient Descent, SGD)

무작위로 데이터 점을 골라 데이터 점 하나를 이용해 가중치를 수정. 이 방법은 가중치에 다양한 시작점 만들 수 있고 여러 지역 극소점 발견할 수 있음.

머신러닝 전반에서 가장 널리 쓰이는 최적화 알고리즘이며 딥러닝에서는 특히 더 많이 쓰임.

경사 하강법이 전체 훈련 데이터에 대해 손실과 경사를 계산하는 데 비해 확률적 경사 하강법은 훈련 데이터 중 하나를 무작위로 선택하여 이 데이터에 대한 경사를 계산한다.

확률적 경사 하강법에서는 훈련 데이터 하나를 대상으로 가중치를 수정하므로 계산 속도는 빠르지만 각각의 가중치 수정이 정확하게 전역 최소점을 향하지 않는다. 전역 최소점에 다가가더라도 그 언저리를 맴돌 뿐 정확하게 전역 최소점에 다다르지 못함.(보통 전역 최소점에 다가가는 정도로 충분)

 

< 확률적 경사 하강법 프로세스 >

 

(1) 훈련 데이터를 무작위로 섞고, 훈련 데이터 하나를 선택한다.

(2) 초기 가중치행렬은 임의의 값을 부여.

(3) 그 가중치행렬의 가장 가파른 방향(미분값)을 계산해냄.

미분값을 구하려면 먼저 해당 가중치행렬에서의 a에 대한(=하나의 훈련데이터에 대한)

오차의 제곱합을 계산한 손실 함수를 구함. -> (10배치)

(4) 학습률만큼 이동하여 수정된 가중치행렬에 대해 다시 손실함수의 미분을 계산.

(5) 또 다른 훈련데이터(b)를 하나 선택해서 1-4과정 반복.

(6) 모든 훈련 데이터에 대해 진행한다. (1에포크)

(7) 1에포크를 n번 반복한다. -> 총 n*10(샘플 수=배치 수) 만큼의 가중치 업데이트가 일어난다.

(5) 미분값이 0에 가까워지는데, 더 유의미하게 미분값이 줄어들지 않을 때의 가중치행렬(w1,w2,,,w25)을 손실을 최소로 하는 가중치행렬이라고 할 수 있음.

(주의)
앞서 배치경사하강법과 동일. 실제 MLP 프로세스대로라면, 가중치를 업데이트하는 (4)과정에서 체인룰을 이용하여 역전파 알고리즘을 적용해야함.

 

< 경사하강법과 확률적 경사 하강법 차이 >

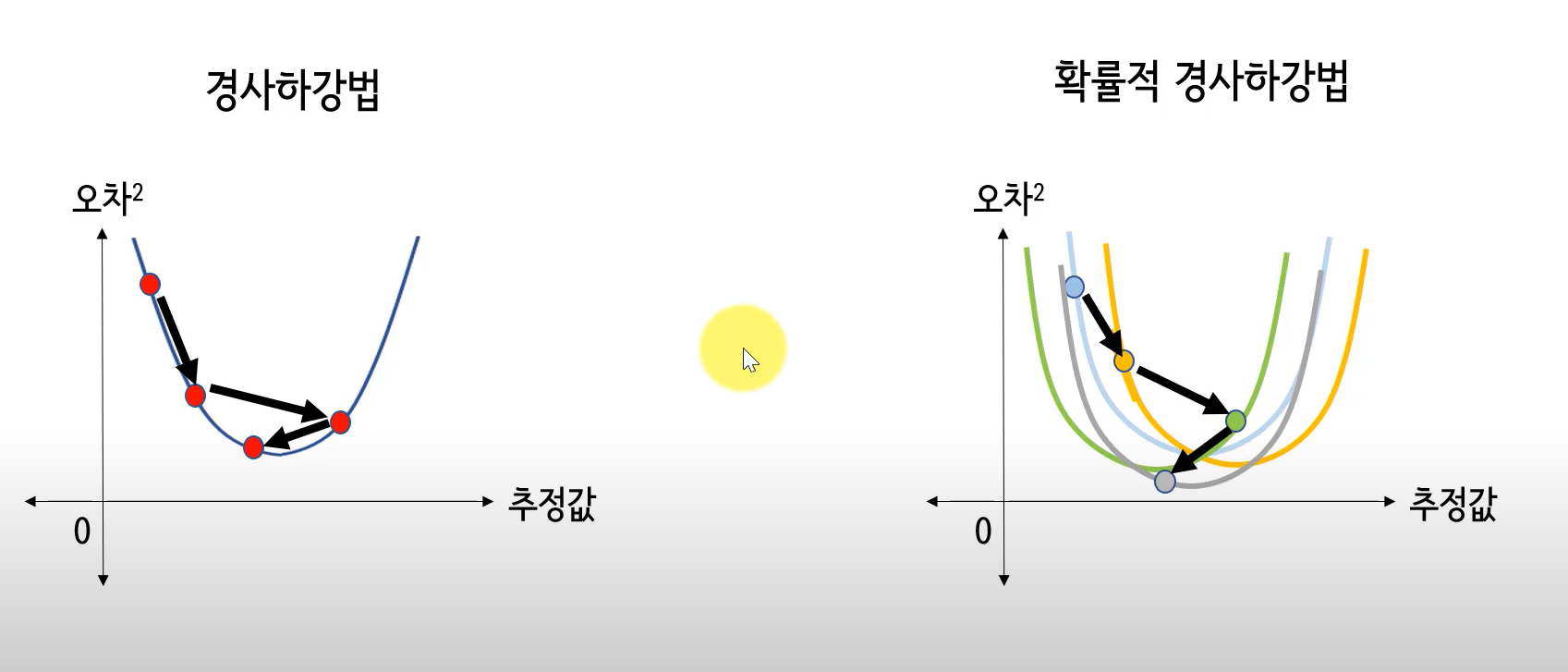
출처 : https://youtu.be/0Lrvk3Fozsc 영상 캡처.

왼쪽 그래프는 배치 경사 하강법, 세로축이 E_total, 가로축은 가중치

오른쪽 그래프는 확률적 경사하강법, 세로축이 E_i(단일 샘플의 손실값), 가로축은 가중치.

 

앞선 경사하강법 프로세스에서 설명한 설정을 빌리자면, 세로축 E_i의 i는 a,b,c,d ... 각 샘플에 대한 오차를 의미

 

최적화 알고리즘은 해당 인공신경망의 오차를 최소로 줄이는 알고리즘이고, 최적화 알고리즘 중에 경사하강법이 있다. 가중치행렬 변화에 따른 손실함수에 대한 함수 그래프에서 오차의 최솟값을 구해야하는데,
배치경사하강법은 모든 훈련데이터(훈련샘플)를 이용하여 인공신경망의 손실값을(손실함수의 출력값) 구하는 반면, 확률적 경사하강법은 하나의 훈련데이터(훈련샘플)를 이용하여 손실값을 구한다.

 

2.6.4 미니배치 경사 하강법(Mini-Bach Gradient Descent, MB-GD)

BGD+SGD의 절충안. 훈련 데이터를 몇 개의 미니배치(미니배치 크기 k=256이 흔함)로 분할한 다음 이 미니배치로부터 경사를 계산. BGD에 비해 가중치 수정 횟수가 더 많은 만큼 더 적은 반복 횟수에서 가중치가 수렴. 벡터 연산을 사용할 수 있으므로 SGD에 비해서도 계산 효율이 좋음.

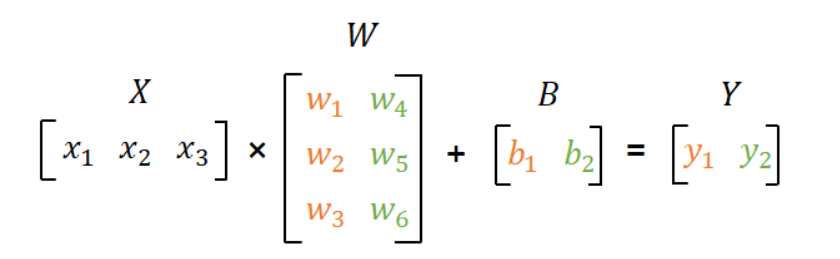
출처 : [딥러닝을 이용한 자연어처리 입문]&nbsp; https://wikidocs.net/150781

-> 훈련데이터 a,b,c,d... = sample #1,2,3,4 ...를 의미.

훈련데이터 전체를 한 번에 병렬 처리하는 것=1배치 연산

 

2.6.5 경사 하강법은 변종이 많다.

네스테로프 가속 경사, RMSprop, Adam, Adagrad

 

2.7 역전파 알고리즘(backpropagation, 역방향 계산 backward pass)

역전파는 신경망 학습의 핵심.

마지막 층에서부터 처음 층의 가중치까지 계산해가는 과정에 chain rule을 이용한 역전파 알고리즘이 쓰인다.

지금까지 배운 신경망 학습은 다음 세 단계를 반복하는 과정(=경사하강법은 아래 3가지 단계를 반복하고, 역전파를 적용하지 않는다.)

1. 순방향 계산 : 선형 결합(가중합)을 계산하고, 선형 결합을 활성화 함수에 입력해서 출력값(y(hat))을 계산.

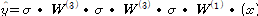
2. 출력값과 정답을 비교해서 오차 함수 또는 손실 함수를 계산한다.(MSE, MAE 등)

3. 경사 하강법 알고리즘을 사용해서 델타w를 계산하고 오차 함숫값을 최적화한다.

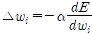
-> 3에서 오차함수 미분값을 구하는 과정에서 역함수가 필요하다. (실제 MLP에서 다음 층의 가중치는 이전 층의 가중치에 종속변수가 되므로(독립변수가 아니다.) 미적분학의 연쇄법칙 chain rule을 통해 이전 층의 가중치를 계산해야한다. 그래서 거꾸로 계산해나가는 과정이므로 역(back)전파라고 이름 붙이게 된 것.)

 

자세한 역전파 내용은 다음 링크를 참고.

https://wikidocs.net/37406