-
[DL for VS #4] CONV kernel, stride, padding, pooling, dropoutMachine Learning/Deep Learning for Vision Systems 2023. 4. 12. 16:33
3.1 다층 퍼셉트론을 이용한 이미지 분류
MNIST 예제를 이용할 것임. MNIST(Modified National Institute of Standards and Technology database) 손글씨 숫자들로 이루어진 대형 데이터베이스MNIST 데이터셋이 깔끔하고 완벽하게 전처리된 상태이기 때문에 MLP 성능(96%)과 CNN 성능(99%)이 비슷하다.
3.1.1 입력층
3.1.2 은닉층
전결합층(fully connected layer, FC = 밀집층, dense layer) 이전 층의 모든 노드가 각기 다음 층의 모든 노드와 연결된 것. 이런 신경망을 전결합 신경망(fully connected network)이라고 함. 노드와 노드를 연결하는 에지(edge)는 해당 노드의 출력에 대한 중요도를 나타내는 가중치.
3.1.3 출력층
분류 문제의 출력층 노드 수 = 분류 대상 클래스 수
3.1.4 MLP 모델 완성하기
3.1.5 MLP로 이미지를 다룰 때의 단점
공간적 특징의 손실
2차원 이미지를 1차원 벡터로 변형하면 이미지 내 공간적 특징이 손실된다. 신경망이 서로 가까이 위치한 픽셀 간의 관계를 알 수 없기 때문에 정보의 손실이 생기는 것.
전결합층
MLP는 절결합층으로 구성되는데, 전결합 구조에서는 어떤 뉴런(노드)이 갖는 파라미터(가중치) 수는 앞 층의 뉴런 수와 같다. 1000x1000 크기의 이미지라면 첫 번째 은닉층의 각 노드마다 백만 개의 파라미터를 갖게 됨.
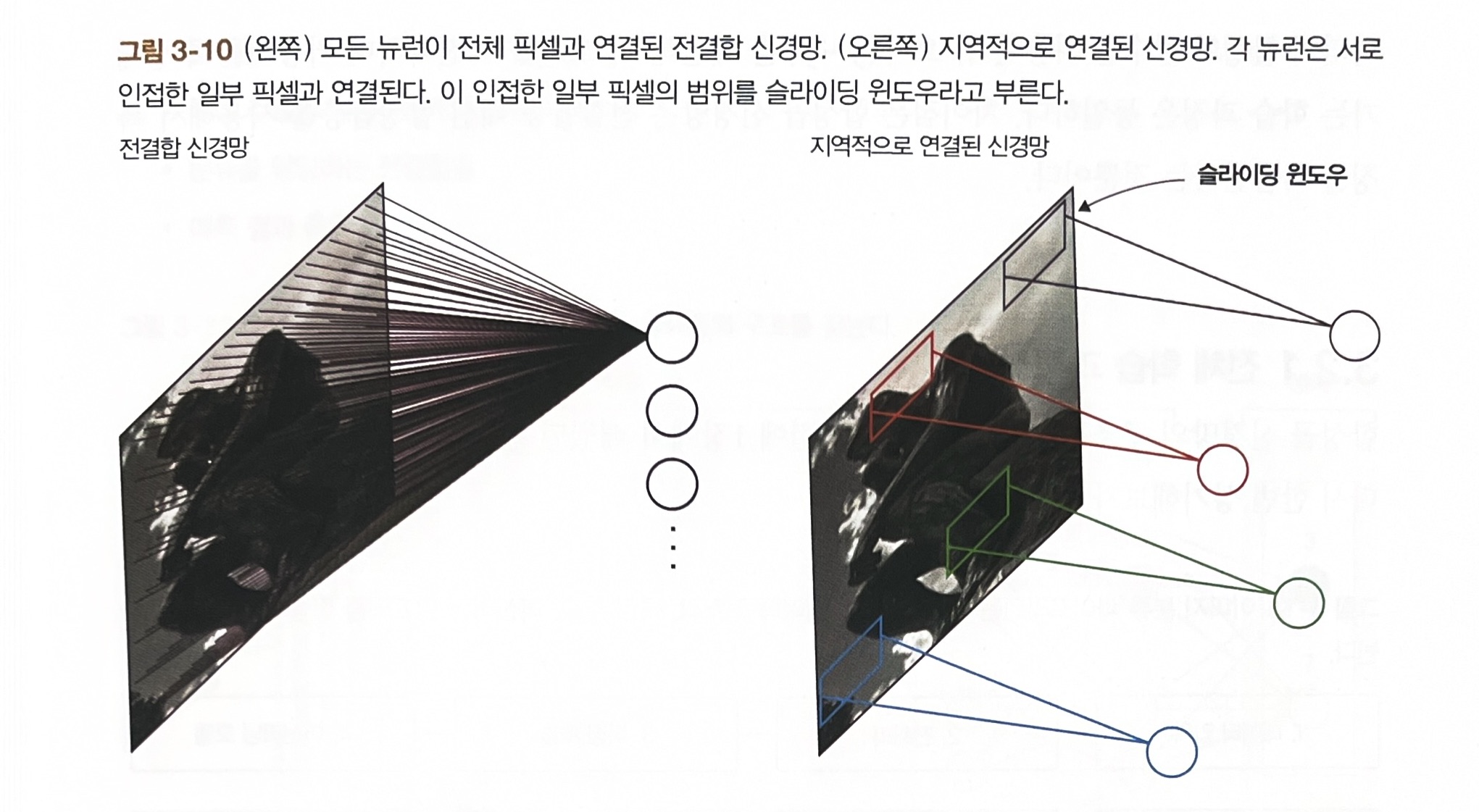
위 두 가지 단점을 개선한 것이 CNN 1번에서 CNN은 2차원 이미지를 그대로 입력할 수 있고, 멀리 떨어진 픽셀보다는 서로 가까운 픽셀끼리 관계가 깊다는 것을 이해할 수 있다. 2번에서 CNN은 지역적으로 연결된(locally connected) 구조의 층을 갖는다. 합성곱 신경망의 노드는 이전 층의 노드 중 일부하고만 연결된다. 지역적 연결을 가진 층은 전결합층에 비해 파라미터 수가 훨씬 적다. 각 뉴런은 서로 인접한 일부 픽셀과 연결되는데, 이 인접한 일부 픽셀의 범위를 슬라이딩 윈도우(sliding window)라고 부른다.
3.2 합성곱 신경망 구조
뉴런으로 은닉층을 구성하고 이 층을 쌓아 신경망을 만든다. 가중치는 무작위 값으로 초기화되며 활성화 함수를 사용한다. 오차(y-y_hat)를 계산해 이 오차를 역전파하며 가중치를 수정해가는 학습 과정은 동일하다. 차이점은 합성곱 신경망은 전결합층 대신 합성곱층을 사용해서 특징을 학습한다는 것뿐이다.
3.2.1 전체 학습 과정
전결합층의 문제는 분류보다는 특징 학습 단계에서 일어난다. 고로 특징 추출을 합성곱층으로 대체하고, 분류는 그대로 전결합층이 맡는다.
CNN의 추상적 구조는 다음과 같다.
-입력층
-특징 추출을 담당하는 합성곱층
-분류를 담당하는 전결합층
-예측 결과 출력
3.3 합성곱 신경망의 기본 요소
1. 합성곱층(convolutional layer, CONV)
2. 풀링층(pooling layer, POOL)
3. 전결합층(fully connected layer, FC)

3.3.1 합성곱층
수학에서 합성곱이란 : 두 함수를 인수로 새로운 함수를 만들어내는 연산.
신경망에서 합성곱이란 : 첫 번째 인수는 입력 이미지고, 두 번째 이미지는 합성곱 필터에 해당.
* 커널(kernel) = 합성곱 필터 – 합성곱 행렬이 바로 가중치.
* 수용영역(receptive field) : 필터가 위치한 입력 이미지상의 범위.
합성곱 연산
*합성곱 필터(커널)는 입력 이미지 위를 이동하며 입력 이미지 전체를 커버한다. 합성곱 필터가 한 번 움직일 때마다 픽셀 단위로 가중합이 계산되어 필터 중심에 해당하는 픽셀의 새로운 값이 결정된다. 이런 방식으로 만들어진 이미지를 특징 맵 또는 활성화 맵(activation map)이라고 한다.
*커널 크기
: 합성곱층을 만들기 위해 필요한 하이퍼파라미터 중 하나. 대부분 정사각형이며 최소 2x2, 최대 5x5 크기의 필터가 사용됨
-> 합성곱 층에 3x3 크기 커널 하나에 유닛은 9개다. 이 층에 3x3 크기의 커널을 하나 추가하면 유닛 수는 18개가 되고, 또 다시 커널을 추가하면 유닛 수는 27개가 된다. 유닛=은닉층의 뉴런=노드
*스트라이드와 패딩
이 두 하이퍼파라미터는 합성곱층의 출력 모양을 결정한다. 사용 목적은 두 가지다. 하나는 이미지에서 중요한 세부 사항을 놓치지 않고 다음 층으로 전달. 둘, 이미지의 공간적 정보를 계산하는 부하를 적절히 감소. 풀링층은 이미지 크기를 줄여서 추출된 특징에 집중.
*스트라이드(stride) : 필터가 입력 이미지 위를 한 번에 이동하는 픽셀 수. 3 이상의 스트라이드 값은 잘 사용하지 않는다. 여러 픽셀을 건너뛰면 출력의 크기가 작아지기 때문.
*패딩(padding) : 흔히 말하는 제로패딩(zero-padding)은 이미지 둘레에 픽셀값이 0인 추가 픽셀을 덧붙이는 것을 말한다. 패딩의 주된 목적은 합성곱 연산을 거친 출력 이미지의 크기를 입력 이미지의 크기와 같게 유지하는 것. 이미지의 크기를 유지하며 합성곱층을 여러 개 사용할 수 있다. 층수가 많은 신경망을 구성할 때 패딩은 특히 중요하다.
3.3.2 풀링층과 서브샘플링
합성곱층 수를 늘리면 출력층의 깊이가 깊어지는 만큼 최적화해야 할 파라미터 수가 늘어난다. 이런 단점을 해결해주는 것이 풀링층.
*풀링(pooling)또는 서브샘플링(subsampling)은 다음 층으로 전달되는 파라미터 수를 감소시키는 방법. 풀링 연산은 최대 또는 평균 같은 통계 함수로 입력 크기를 축소해 다음 층으로 전달되는 파라미터 수를 감소시킨다. 일종의 이미지 압축 프로그램. 중요한 특징은 유지하면서 이미지의 해상도를 떨어뜨리는 것.
*최대 풀링
합성곱 커널과 비슷하게 최대 풀링 커널에도 윈도우 크기와 스트라이드가 있다. 다만 최대 풀링은 행렬에 별도의 가중치가 없다. 특징 맵의 크기는 작아지지만 특징 맵 개수는 유지된다.

*전역 평균 풀링 (global average pooling)
특징 맵 크기를 극단적으로 줄이는 압식이다. 윈도우 크기와 스트라이드를 설정하지 않고 전체 특징 맵 픽셀값의 평균을 구한다.

*풀링, 스트라이드, 패딩 비교
풀링과 스트라이드만 잘 조절하면 패딩 필요없다고도 함.<Starving for Simplicity: the all convolutional Net>에서는 풀링층을 완전히 배제하고 합성곱층만을 사용하기도 함. 중간 중간 스트라이드를 크게 설정한 합성곱층을 배치한 것. 생성적 적대 신경망과 같은 생성 모델을 학습할 때는 풀링층을 배제하는 방법이 효과적이긴 하다.
3.3.3 전결합층
합성곱층과 풀링층으로 학습 후 대롱과 같은 모양으로 추출된 특징을 얻었고, 이렇게 추출된 특징을 사용해서 실제로 이미지를 분류할 때 MLP를 사용.
*MLP, 전결합층, 밀집층, 피드포워드 신경망 등은 일반적인 신경망 구조를 나타내는 용어로 서로 바꿔 써도 무방.
*프로세스 :
1) 1차원 벡터 입력 : 대롱처럼 추출된 특징 맵(5x5x40)을 MLP에 입력하려면 (1,n) 모양(가로로 긴 행렬)의 1차원 벡터로 변환해야 한다. (5x5x40)->(1,1000) 1x1 행렬 1000개
2) 은닉층 : 하나 이상의 전결합층을 갖는다. 전결합층은 다시 하나 이상의 뉴런으로 구성됨.(MLP구성할때와 동일)
3) 출력층 : 활성화 함수로 소프트 맥스 함수 사용. 출력층의 유닛 수는 분류 클래스 수.
3.5.2 드롭아웃층이란
드롭아웃층은 과적합을 방지하기 위한 수단 중 가장 널리 쓰인다. 층을 구성하는 뉴런(노드)의 일정 비율을 비활성화한다. 특정 노드가 다른 노드를 지배해 큰 실수를 일으키는 일으 방지하고 모든 노드가 동등하게 성능에 기여하는 데 도움이 된다.
드롭아웃을 일종의 앙상블 학습 기법으로 볼 수 있다. 앙상블 학습은 여러 개의 약분류기를 독립적으로 학습시킨 후 이들의 예측 결과를 통합해 전체 결과로 삼는 기법이다.
3.5.4 CNN 구조 중 어디에 드롭아웃층을 끼워 넣어야 할까
추출된 특징의 1차원 벡터 변환이 끝난 다음부터 마지막 출력층 사이에 배치하는 것이 일반적이고 경험적으로 전결합층에 적용하는 것이 효과가 좋다고 알려짐.
keras에서 드롭아웃층을 정의할 때 rate를 인수로 받는다. rate는 비활성화할 노드의 비율을 의미한다. 비활성화되는 논드는 새로운 에포크마다 바뀐다. 무작위로 선택되므로 특정 노드가 더 자주 비활성화될 수 있지만 괜찮다. 여러 번 반복하다 보면 모든 뉴런이 거의 동등한 비율로 비활성화된다. 이 비율은 CNN을 미세 조정하는 하이퍼파라미터이기도 하다.
'Machine Learning > Deep Learning for Vision Systems' 카테고리의 다른 글
[DL for VS #6] 성능 지표 - 정확도, 혼동 행렬, 정밀도, 재현율, F-점수, 시각화 예제 (0) 2023.04.12 [DL for VS #5] 컬러 이미지 합성곱 연산 실습 (0) 2023.04.12 [DL for VS #3] 최적화 알고리즘-(배치, 확률적, 미니배치)경사하강법, 역전파 알고리즘 (1) 2023.04.08 [DL for VS #2] 순방향 계산 과정, 오차함수-평균제곱오차(MSE), 교차엔트로피, 오차와 가중치 관계(최적화 문제) (0) 2023.04.07 [DL for VS #1] 활성화 함수 : sigmoid, softmax, tanh, ReLU, Leaky ReLU (0) 2023.04.07