[DL for VS #2] 순방향 계산 과정, 오차함수-평균제곱오차(MSE), 교차엔트로피, 오차와 가중치 관계(최적화 문제)

2.4.1 순방향 계산 과정

출처 : 비전시스템을 위한 딥러닝 p.93

2.5 오차함수

비용함수(cost function) 또는 손실 함수(loss function)라고 불림.

신경망의 예측 결과가 바람직한 출력과 비교해서 얼마나 ‘동떨어졌는지’ 측정하는 수단.

손실값 크면 모델의 정확도가 낮다는 뜻.

 

2.5.2. 오차함수 필요성

최적화 문제와 관계됨. 최적화 문제는 오차 함수를 정의하고 파라미터(가중치)를 조정해서 오차 함수가 계산하는 오차를 최소가 되도록 하는 문제.

오차를 최소로 만드는 과정을 오차 함수 최적화(error function optimization)라고 함.

오차의 값은 항상 양수. 목표치에서 얼마나 떨어졌는지가 중요.

 

2.5.4 평균제곱오차(Mean Squared Error,MSE)

출력값이 실수인 회귀 문제에서 널리 사용하는 오차 함수.

각 데이터 점의 오차를 제곱해서 평균을 구함.

 

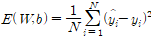
W	가중치 행렬, 쌔타로 표기하기도 함.
b	편향 벡터
N	학습 데이터 수(-> 훈련데이터 개수를 뜻하는 게 아니라, 출력 층의 노드 수)
y(hat)	출력된 예측 결과, 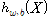  로 표기하기도 함.
y(hat)-y	일반적으로 오차 또는 잔차라고 부름.

오차가 양의 값이라 계산이 간편.

오차를 제곱하기 때문에 예욋값에 민감. 장점, 단점이기도 함. 예욋값을 논리적으로 설명하려 할 때 도움됨.

중위값을 중시해야하는 목적에서는 절대제곱오차(Mean Absolute error, MAE)를 사용. 절대제곱오차는 오차의 절댓값의 평균이다.

2.5.5 교차 엔트로피(cross-entropy)

두 확률 분포 간의 차이를 측정할 수 있다는 특성 덕분에 주로 분류문제에서 많이 사용한다.

예를 들어 ‘개’가 찍힌 이미지를 세 가지 클래스(개, 고양이, 물고기) 중 하나로 분류하려고 한다.

 

* 이 이미지의 실제 확률 분포는 아래와 같다.

Probability(고양이)	P(개)	P(물고기)
0.0	1.0	0.0

 

*머신러닝 모델의 예측 결과로 얻은 확률 분포는 아래와 같다고 하자.

Probability(고양이)	P(개)	P(물고기)
0.2	0.3	0.5

실제 확률 분포와 예측 확률 분포는 얼마나 가까울까? 교차 엔트로피는 다음과 같다.

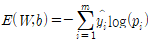
y : 대상 확률 분포

p : 예측 확률 분포

m : 클래스 수

교차 엔트로피 정의대로 머신러닝 모델의 예측 결과로 얻은 확률 분포표를 토대로 손실값을 계산하면 아래와 같다.

E = -(0.0 * log(0.2) + 1.0 * log(0.3) + 0.0 * log(0.5)) = 1.2

 

*신경망을 다시 학습시키고 다시 예측해봤더니 아래와 같은 예측값이 나왔다고 하자.

Probability(고양이)	P(개)	P(물고기)
0.3	0.5	0.2

손실값을 다시 계산해보면 아래와 같다.

E = -(0.0 * log(0.3) + 1.0 * log(0.5) + 0.0 * log(0.2)) = 0.69

손실값이 더 낮아진 것을 확인할 수 있다.(예측 모델의 성능이 상승했다.)

 

* 모든 학습 샘플 n에 대해 교차 엔트로피를 아래와 같이 계산할 수 있다.

 

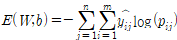
2.5.6 오차와 가중치의 관계

입력이 하나인 퍼셉트론을 생각해보자.

입력 x= 0.3, 레이블(정답) y=0.8, 이 퍼셉트론의 예측 결과 y(hat)은 다음과 같다

y(hat)=w*x=w*0.3

 

오차(error) =

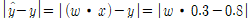
-> 가중치를 조절해서 오차를 줄여야한다.

오차함수의 가장 큰 이점은 신경망의 학습을 오차를 최소화하는 최적화 문제로 바꿀 수 있다는 것.

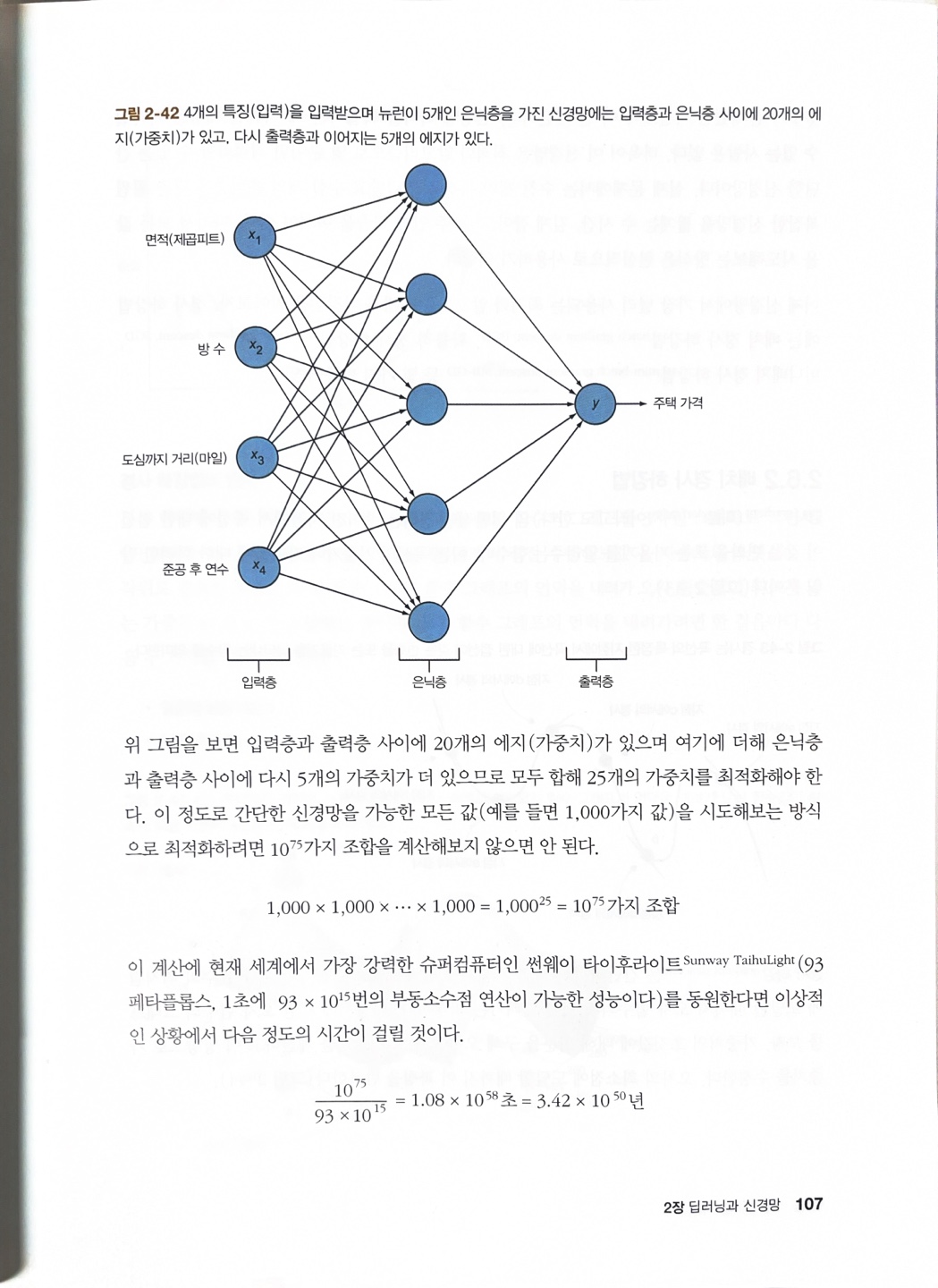
출처 : 비전 시스템을 위한 딥러닝 p.107

 

* 최적화 알고리즘이 필요한 이유.

 

예를들어 25개의 가중치(w_1, w_2, w_3, ... , w_25)에서 각 가중치당 1000가지의 샘플(훈련데이터)을 뽑아낸다고 할 때,

(예를들어, w_1 = 0~999, w_2 = 0~999,,, w_25 = 0~999)

1000 x 1000 x ... x 1000=1000^25=10^75가지 조합을 계산해야한다.

이는 지구 최강의 컴퓨터 성능을 자랑하는 컴퓨터라 해도 우주 존재 시간보다 더 걸린다.