Batch Normalization (배치정규화)

* BN이 효과적인 이유

공변량 시프트(covariate shift) 문제

 데이터셋 X를 레이블 y에 매핑하도록 모델을 학습한 후 X의 분포가 변화한 경우를 공변량 시프트라고 한다. 공변량 시프트가 발생하면 모델을 다시 학습해야 할 수도 있다.

예를 들면, 흰색 고양이로 치워친 훈련 데이터로 학습된 고양이 분류기에 흰색이 아닌 다른 색 고양이 이미지를 분류할 때 좋은 성능이 나오지 않는 경우로, 이러한 입력데이터 분포의 변화를 공변량 시프트라고 한다.

 

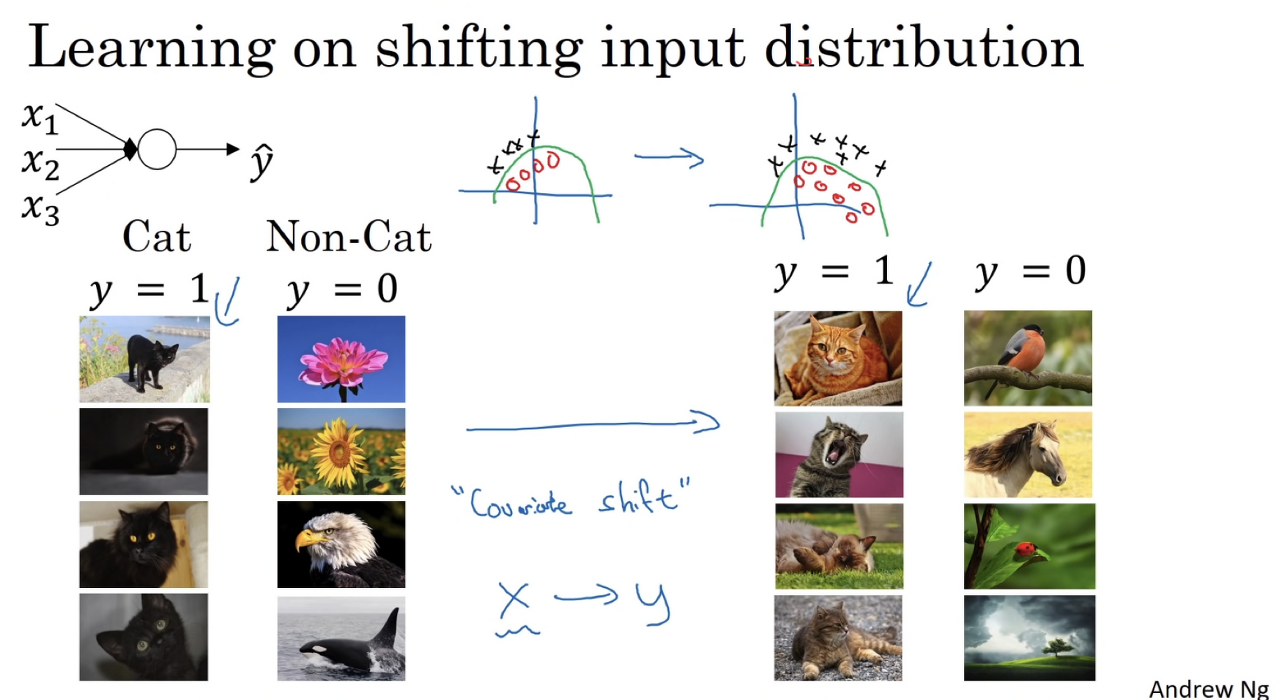
신경망에서 발생하는 공변량 시프트

4개의 층을 가진 MLP를 예로 들면, L3의 관점에서 L1의 파라미터(w,b) 변화에 의해  L3층의 입력에 해당하는 L2층의 출력값들이 변화하고 있다. 즉, 은닉층 내부에서 공변량 시프트가 발생하는 것이다. 

배치 정규화의 원리

세르게이 이요페(Sergey Ioffe)와 크리스티안 세게디(Christian Szegedy)가 2015년 논문에서 공변량 시프트를 완화하기 위한 대책으로 배치 정규화를 제안했다. 배치 정규화는 각 층의 활성화 함수 앞에 다음 연산을 추가하는 방법이다.

• 입력의 평균을 0으로 조정
• 평균이 0으로 조정된 입력을 정규화
• 연산 결과의 배율 및 위치 조정

 

* 배치 정규화의 수학적 원리

1. 현재 입력 중인 미니배치의 입력값의 평균을 0으로 조정하려면 입력의 평균과 표준편차를 계산해야한다.

m이 배치 내 데이터 수일 때 미니배치의 평균(mu_B)과 표준편차(sigma_B)는 다음과 같이 계산한다.

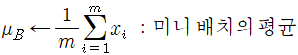
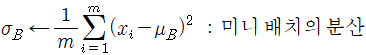
2. 입력을 정규화한다. 여기서 x(hat)은 평균이 0이며 정규화된 입력이다.

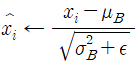
새로운 변수 epsilon이 추가되었다. 이 변수는 일부 추정치에서 sigma가 0일 경우 0으로 나누는 것을 피하기 위한 충분히 작은 값이다(일반적으로 10^-5 정도 사용).

 

3. 배율 및 위치를 조정한다. 정규화된 입력에 gamma를 곱해 배율을 조정하고 beta를 더해 위치를 조정한 y_i를 계산한다.

배치 정규화를 적용하면 신경망에 2개의 새로운 파라미터 gamma와 beta가 도입된다. 따라서 최적화 알고리즘이 가중치와 함께 이 두 가지 파라미터를 수정한다. 학습 초기에 최적의 배율과 오프셋을 찾기까지는 약간 학습 속도가 느리게 느껴지지만 최적의 값을 찾고 나면 학습이 눈에 띄게 빨라진다.

 

* 배치 정규화 적용 위치

• Conv → Batch Norm → Activation → Dropout

 

* 사전에 알아 둘 통계지식.

• 모집단의 확률분포가 정규분포이면 확률변수 $\bar{X}$ 는 sample size(n의 크기)에 관계없이 정규분포 N(m, $\frac{\sigma^2}{n}$)을 따른다.
• 모집단의 확률분포가 정규분포가 아니더라도 표본의 크기 n이 충분히 크면 확률변수 $\bar{X}$ 는 근사적으로 정규분포 N(m, $\frac{\sigma^2}{n}$)을 따른다.(중심극한정리)

 

 

* 표기법 정리

• g = activation function
• z = 입력값에 가중치와 편향을 계산해준 값
• 모평균을 $\mu$, 모분산을 $\sigma^2$ 라고 하자.
• 총 데이터 수가 3200개이고, batch size =32이면, 하나의 배치에 32개의 샘플이 있고 100개의 mini batch로 나뉜다.→mini-batch size = 32는 표본크기(sample size)= 32로 임의 추출한 상황과 같다.
• 미니 배치 내의 32개의 샘플의 평균은 표본평균($\bar{X}$)이고, 미니배치 내의 32개의 샘플의 분산은 표본분산($S^2$)이다.
• superscript 정리
  • [1] : hidden layer의 1번째 층을 의미.
  • {1} : 32개의 mini-baches에서 1번째 mini-batch를 의미.
  • (1) : 1개의 mini-batch에서 1번째 샘플을 의미

 

 

 

* Training시 BN 동작 설명

1. 미니 배치 하나에 대한 표본평균 $\bar{X}B^{\{1\}}=\frac1{32}\sum{k=1}^1\sum_{i=1}^{32}z^{(i)}$
   • $\sum_{k=1}^1$ 는 sample size =1을 명시적으로 표기해준 것이다.
   • 1개의 미니배치=32개 샘플에 대한 평균 → sample distribution (표본분포)이면서, sample size(n)=1인 sampling distribution(표집분포)
     
     
2. 분산 $S_B^{2\{1\}} = \frac1{31}\sum_{k=1}^1\sum_{i=1}^{32}(z^{(i)}-\bar{X_B}^{\{1\}})$
   • 1개의 미니배치 =32개 샘플에 대한 분산
   • 분산에 경우 biased estimate이므로 Bessel’s Correction(베셀 보정)을 적용해준다.
   • 2023.12.03 - [Mathematics/statistics] - 불편추정량, 편의추정량
     
     
3. normalize $\frac {z_i^{\{1\}} - \bar{X}_B^{\{1\}}} {\sqrt{S_B^{2\{1\}}+\epsilon}} = \hat{z_i}^{\{1\}}$ 를 구한다.
   1. 여기서 i는 100개의 mini-batch 중 1개의 mini-batch(32개의 샘플)에 대해 정규화를 진행한 것! (i는 1~32 값을 갖는다.)
   2. [1]layer층의 1개의 노드에 대해 32번의 normalize를 계산한다.
   3. 표준화(Standardization)과 같은 과정이다. 표준화를 거치면 표준정규분포N(0,1)을 따른다.
      
      
4. $\gamma \hat{z_i} + \beta = \tilde{z_i}$
   • 노드 당 두 개($\gamma, \beta$)의 파라미터가 추가 된다.

 

 

 

* BN 중간 리뷰

• 모집단이 정규분포를 따를 것이라고 가정한다.
  • 표준화를 통과할 때 확률변수는 정규분포를 따라야한다. sample size가 충분히 크면, 중심극한정리에 의해 표집분포는 정규분포를 따를 것이다. 그러나 sample size=1로, 충분치 않다. 여기서는 모집단이 정규분포를 따를 것이라는 가정하에 표준화를 진행한다.
    
    
• 기존 bias는 learning하지 않아도 된다.
  • z=Wx+b에서, BN의 수식을 보면 $\gamma \hat{x_i} + \beta = y_i$ 이고, $\beta$ 가 bias training을 해주므로 굳이 b를 학습시킬 필요가 없다. 즉, g(BN(Wx))가 된다.
    
    
• $\gamma, \beta$ 에 대한 직관적 이해
  • 극도로 퍼진 데이터를 N(0,1)로 모으고, 다시 전체적으로 평행이동 및 스케일링 해줌으로써, 비선형성의 효과를 받을 수 있는 상태로 세팅해준다.

 

 

 

* Test시 BN 동작 설명

Test시에는 하나의 샘플만 입력값으로 들어오기 때문에 training때 계산했던 각각의 미니배치의 평균을 이용한다.

 

1. 모든 미니 배치에 대한 평균을 구한다. $E[\bar{X_B}]=\frac1{100}\sum_{k=1}^{100}\sum_{i=1}^{32}z^{(i)}=\frac{1}{100}\sum_{k=1}^{100} \bar{X}_B^{\{k\}}$
   • 32개 샘플의 평균들의 100세트 평균을 구함. → sample size=32인, samplig distribution (표집분포)
   • 평균은 불편추정량(unbiased estimate)이고, sample size가 충분히 크므로, $E[\bar{X_B}] = \mu$ 가 성립한다.
   • 실제로는 산술평균이 아닌 EMA(Exponential moving average)를 구한다.
   • 2023.11.22 - [Mathematics/Calculus] - EMA(Exponential Moving Average, EMA) 지수이동평균
     
     
2. 분산 : $E[S_B^2]=\frac1{99}\sum_{k=1}^{100}\sum_{i=1}^{32}(z^{(i)}-\bar{X_B}^{\{n\}})=\frac1{99}\sum_{k=1}^{100} (\bar{X_B}^{\{k\}}-E[\bar{X_B}])^2$
   • 32개 샘플의 평균들의 100세트 분산을 구함.
   • 분산은 편의추정량(biased estimator)이므로, n대신 n-1로 나누어 줘야지 $E[S_B^2]=\sigma^2$ 을 만족한다.
   • 마찬가지로 실제로는 산술평균이 아닌 EMA을 구한다.
     
     
3. normalize $\frac {z - E[\bar{X}_B]} {\sqrt{E[S_B^2]+\epsilon}} = \hat{z}$
   • test 시에는 하나의 입력값 z만 입력된다.
     
     
4. $\gamma \hat{z} + \beta = \tilde{z}$ 계산. 학습된 $\gamma$, $\beta$ 를 사용해서 BN을 적용한 $\tilde{z}$ 을activation function에 입력값으로 사용한다.

 

 

* 참고

https://www.youtube.com/watch?v=m61OSJfxL0U&t=361s

https://www.youtube.com/watch?v=5qefnAek8OA