[DL for VS #9] LeNet-5

5.1 CNN의 디자인 패턴

 

* 첫 번째 패턴 : 특징 추출과 분류.

• 합성곱 신경망은 크게 특징 추출을 맡는 부분(일련의 합성곱층)과 분류를 맡는 부분(일련의 전결합층)으로 나뉜다.

* 두 번째 패턴 : 이미지 깊이(색상 채널)는 증가, 크기는 감소.

• 입력층에서 색상 채널에 해당한 깊이가 합성곱층에서는 특징맵으로 바뀌어 깊이가 계속 증가한다.
• 입력 이미지 모양 = 높이x폭x채널({r,g,b}=3)
• 이미지 모양 = 높이 x 폭 x 특징맵수

* 세 번째 패턴 : 전결합층.

• 앞의 두 패턴만큼 반드시 지켜지지는 않음.
• 대부분 전결합층은 유닛 수가 같거나 이어지는 층에서 점차 유닛 수가 감소하는 패턴을 보임. 이어지는 층에서 유닛 수가 증가하는 경우는 매우 드물다. 

5.2 LeNet-5

1998년 르쿤의 연구진은 합성곱 신경망의 선구자적 구조인 LeNet-5를 발표했다. 가중치를 가진 5개의 층(3개의 합성곱층과 2개의 전결합층)으로 구성되었기 때문에 이러한 이름이 붙었다.

신경망의 깊이는 대개 '가중치를 가진 층수'를 기준으로 한다(가중치를 가진 층수가 모델의 계산 복잡도와 직결되기 때문). 풀링층은 가중치가 없으므로 층수에 포함되지 않는다. AlexNet은 5개의 합성곱층과 3개의 전결합층으로 구성되었으므로 층수가 8이다.

 

* LetNet-5 논문 

Y. Lecun, L. Bottou, Y. Bengio. P. Haffner, 'Gradient-Based Learning Applied to Document Recognition., Proceedings of the IEEE 86 (11): 2278-2324, http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf

LeNet-5의 내용 대부분은 논문의 섹션 2와 3에 집중되어 있으며, 그 이후 부분은 그래프 변환 네트워크(최근에는 잘 쓰이지 않는다)를 설명한다. 필자는 AlexNet의 논문을 읽고 그 다음에 VGGNet의 논문 그다음에 LeNet-5 순서로 읽을 것을 추천한다. (다른 논문을 먼저 읽어봐야 고전의 맛을 제대로 느낀다고...)

 

5.2.1 LeNet 구조

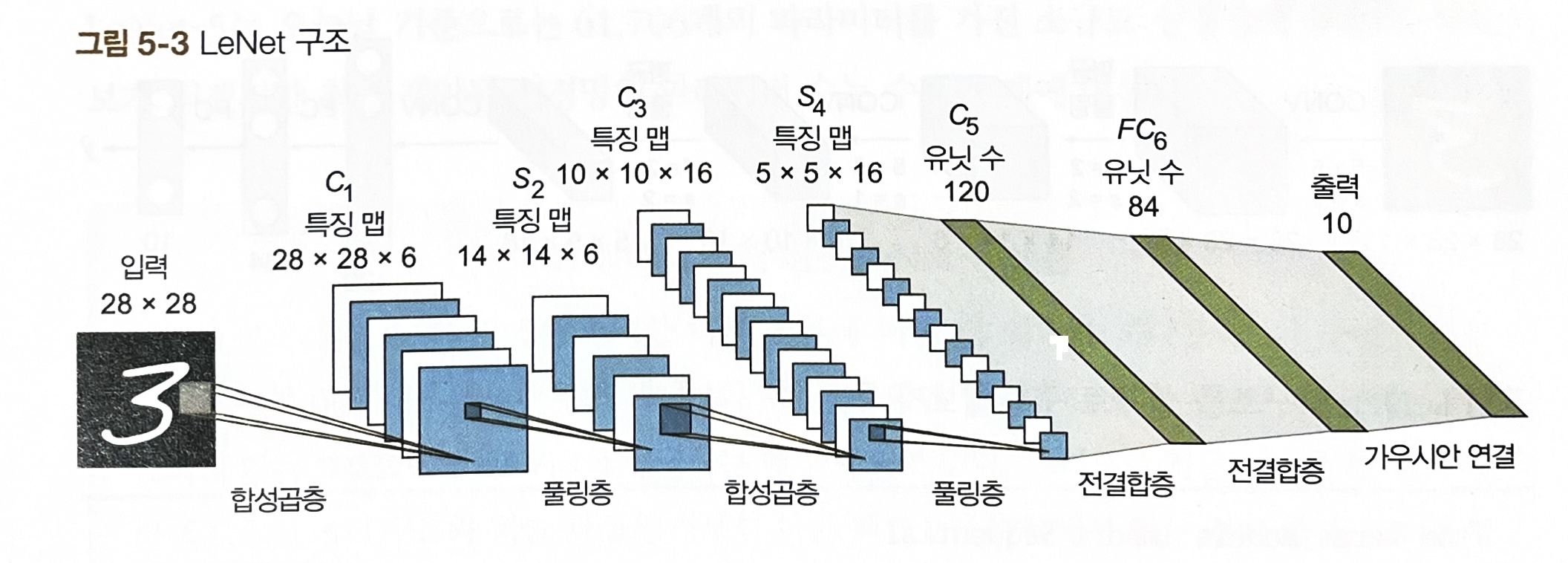
입력 이미지 => C1 => TANH => S2 => C3 => TANH => S4 => C5 => TANH => FC6 => SOFTMAX7

C는 합성곱층, S는 풀링층(서브샘플링층), FC는 전결합층이다.

당시에는 은닉층 유닛의 활성화 함수로 tanh와 시그모이드 함수를 사용하는 것이 일반적이었다.

 

5.2.2 케라스로 LeNet-5 구현하기

 

위 논문 6~8쪽에 실린 LeNet-5 구조에 대한 내용을 따라 LeNet-5를 케라스로 구현하자. 논문에서 확인할 수 있는 LeNet-5 구조의 핵심은 다음과 같다.

• 각 합성곱층의 필터 수 : 각 합성곱층의 깊이(필터 수)는 다음과 같다. C1: 6, C3: 16, C5: 120
• 각 합성곱층의 커널 크기 : 논문에서는 kernel_size의 값을 5 x 5라고 언급했다.
• 풀링층(서브샘플링층) :  각 합성곱층 뒤에는 풀링층이 배치된다. 수용 영역의 크기는 2 x 2다.(pool_size로는 2). LeNet-5의 풀링층에는 평균 풀링이 사용됐다. 
• 활성화 함수 : tanh함수를 은닉층의 활성화 함수로 사용한다. 당시에는 대칭 함수가 시그모이드 함수에 비해 가중치가 더 빨리 수렴한다고 생각했기 때문이다.